
【题目】如图所示,已知点M(0,2),直线y= ![]() x+4与两坐标轴分别交于A,B两点,P、Q分别是线段OA,AB上的动点,则PQ+MP的最小值是 .
x+4与两坐标轴分别交于A,B两点,P、Q分别是线段OA,AB上的动点,则PQ+MP的最小值是 . 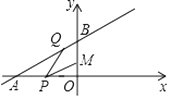
【答案】3 ![]()
【解析】解:如图,点M关于x轴的对称点N(0,﹣2),过点N作NQ⊥AB交OA于P,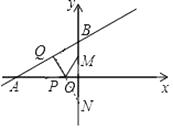
则NQ=PQ+PM的最小值,
∵直线y= ![]() x+4与两坐标轴分别交于A,B两点,
x+4与两坐标轴分别交于A,B两点,
∵B(0,4),∠OAB=30°,
∴∠ABO=60°,BN=4+2=6,
∴在Rt△BQN中,QN=sin60°BN=3 ![]() ,
,
∴PM+MN的最小值是 3 ![]() .
.
所以答案是 3 ![]() .
.
【考点精析】本题主要考查了一次函数的性质和一次函数的图象和性质的相关知识点,需要掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小;一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远才能正确解答此题.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两条轮船同时从港口A出发,甲轮船以每小时30海里的速度沿着北偏东60°的方向航行,乙轮船以每小时15海里的速度沿着正东方向行进,1小时后,甲船接到命令要与乙船会合,于是甲船改变了行进的速度,沿着东南方向航行,结果在小岛C处与乙船相遇.假设乙船的速度和航向保持不变,求:
(1)港口A与小岛C之间的距离;
(2)甲轮船后来的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简再求值:
(1)3(x2-2x-1)-4(3x-2)+2(x-1),其中x=﹣3;
(2)2a2﹣[![]() (ab﹣4a2)+8ab]﹣
(ab﹣4a2)+8ab]﹣![]() ab,其中a=1,b=
ab,其中a=1,b=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
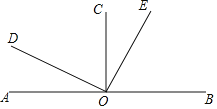
【题目】如图,已知直线AB上一点O,OC⊥AB,OD⊥OE, 若∠COE=![]() ∠BOD.
∠BOD.
(1)求∠COE, ∠BOD, ∠AOE的度数.
(2)若OF平分∠BOE,求∠AOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=10,BC=8,P为AD的中点,将△ABP沿BP翻折至△EBP(点A落到点E处),连接DE,则图中与∠APB相等的角的个数为( ) 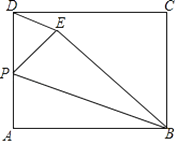
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小华在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进30米到达C处,又测得顶部E的仰角为60°,求大楼EF的高度.(结果精确到0.1米,参考数据 ![]() =1.732)
=1.732)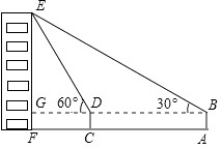
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,设正方体ABCD-A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从点A出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA1→A1D1→…,白甲壳虫爬行的路线是AB→BB1→…,并且都遵循如下规则:所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交(其中n是正整数),那么当黑、白两个甲壳虫各爬行完第2013条棱分别停止在所到的正方体顶点处时,它们之间的距离是 .
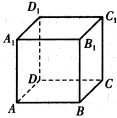
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】生态公园计划在园内的坡地上种植一片有A、B两种树的混合林,需要购买这两种树苗共100棵.假设这批树苗种植后成活95棵,种植A、B两种树苗的相关信息如下表:

(1)求购买这两种树苗各多少棵?
(2)求种植这片混合林的总费用需多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数y=k1x的图象与反比例函数y= ![]() 的图象的一个交点是(2,3).
的图象的一个交点是(2,3).
(1)求出这两个函数的表达式;
(2)作出两个函数的草图,利用你所作的图形,猜想并验证这两个函数图象的另一个交点的坐标;
(3)直接写出使反比例函数值大于正比例函数值的x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com