
【题目】如图,矩形ABCD中,AB=10,BC=8,P为AD的中点,将△ABP沿BP翻折至△EBP(点A落到点E处),连接DE,则图中与∠APB相等的角的个数为( ) 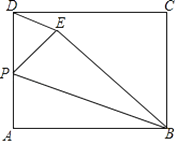
A.1个
B.2个
C.3个
D.4个
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】解答下列各题
(1)化简并求值:-(3a2-4ab)+[a2-![]() (a+2ab)] ,其中a=-2,b=1
(a+2ab)] ,其中a=-2,b=1
(2)已知多项式(2x2+ax-y+6)-(2bx2-3x+5y-1)的值与字母x的取值无关,求a、b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图l,BD是矩形ABCD的对角线,∠ABD=30![]() ,AD=1.将△BCD沿射线BD方向平移到△B'C'D'的位置,使B'为BD中点,连接AB’,C'D,AD’,BC’,如图2.
,AD=1.将△BCD沿射线BD方向平移到△B'C'D'的位置,使B'为BD中点,连接AB’,C'D,AD’,BC’,如图2.
(1)求证:四边形AB'C'D是菱形:
(2)四边形ABC'D'的周长为____:
(3)将四边形ABC'D’沿它的两条对角线剪开,用得到的四个三角形拼成与其面积相等的矩形,直接写出可能拼成的矩形的周长.
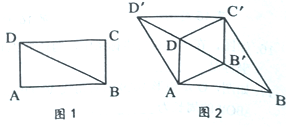
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】考试前,同学们总会采用各种方式缓解考试压力,以最佳状态迎接考试.某校对该校九年级的部分同学做了一次内容为“最适合自己的考前减压方式”的调查活动,学校将减压方式分为五类,同学们可根据自己的情况必选且只选其中一类.学校收集整理数据后,绘制了图1和图2两幅不完整的统计图,请根据统计图中信息解答下列问题:
(1)这次抽样调查中,一共抽查了多少名学生?
(2)请补全条形统计图;
(3)请计算扇形统计图中“享受美食”所对应扇形的圆心角的度数;
(4)根据调查结果,估计该校九年级500名学生中采用“听音乐”来减压方式的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为60°和35°,已知大桥BC的长度为100m,且与地面在同一水平面上.求热气球离地面的高度. (结果保留整数,参考数据:sin35°≈ ![]() ,cos35°≈
,cos35°≈ ![]() ,tan35°≈
,tan35°≈ ![]() ,
, ![]() ≈1.7)
≈1.7)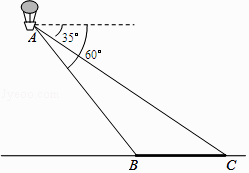
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB表示路灯,当身高为1.6米的小名站在离路灯1.6的D处时,他测得自己在路灯下的影长DE与身高CD相等,当小明继续沿直线BD往前走到E点时,画出此时小明的影子,并计算此时小明的影长. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com