
【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
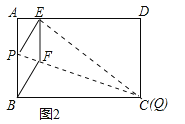
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.

【答案】(1)证明见解析;(2)①菱形BFEP的边长为![]() cm;②点E在边AD上移动的最大距离为2cm.
cm;②点E在边AD上移动的最大距离为2cm.
【解析】试题分析:(1)由折叠的性质得出PB=PE,BF=EF,∠BPF=∠EPF,由平行线的性质得出∠BPF=∠EFP,证出∠EPF=∠EFP,得出EP=EF,因此BP=BF=EF=EP,即可得出结论;
(2)①由矩形的性质得出BC=AD=5cm,CD=AB=3cm,∠A=∠D=90°,由对称的性质得出CE=BC=5cm,在Rt△CDE中,由勾股定理求出DE=4cm,得出AE=AD﹣DE=1cm;在Rt△APE中,由勾股定理得出方程,解方程得出EP=![]() cm即可;
cm即可;
②当点Q与点C重合时,点E离点A最近,由①知,此时AE=1cm;当点P与点A重合时,点E离点A最远,此时四边形ABQE为正方形,AE=AB=3cm,即可得出答案.
试题解析:解:(1)∵折叠纸片使B点落在边AD上的E处,折痕为PQ,∴点B与点E关于PQ对称,∴PB=PE,BF=EF,∠BPF=∠EPF.又∵EF∥AB,∴∠BPF=∠EFP,∴∠EPF=∠EFP,∴EP=EF,∴BP=BF=EF=EP,∴四边形BFEP为菱形;
(2)①∵四边形ABCD是矩形,∴BC=AD=5cm,CD=AB=3cm,∠A=∠D=90°.∵点B与点E关于PQ对称,∴CE=BC=5cm.在Rt△CDE中,DE=![]() =4cm,∴AE=AD﹣DE=5cm﹣4cm=1cm.
=4cm,∴AE=AD﹣DE=5cm﹣4cm=1cm.
在Rt△APE中,AE=1,AP=3﹣PB=3﹣PE,∴EP2=12+(3﹣EP)2,解得:EP=![]() cm,∴菱形BFEP的边长为
cm,∴菱形BFEP的边长为![]() cm;
cm;
②当点Q与点C重合时,如图2:
点E离点A最近,由①知,此时AE=1cm;
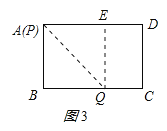
当点P与点A重合时,如图3所示:
点E离点A最远,此时四边形ABQE为正方形,AE=AB=3cm,∴点E在边AD上移动的最大距离为2cm.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
【题目】某化肥厂去年四月份生产化肥500吨,因管理不善,五月份的产量减少了![]() ,从六月起强化管理,该厂产量逐月上升,七月份产量达到648吨.
,从六月起强化管理,该厂产量逐月上升,七月份产量达到648吨.
![]() 该厂五月份的产量为______吨;
该厂五月份的产量为______吨;![]() 直接填结果
直接填结果![]()
![]() 求六、七两月产量的平均增长率.
求六、七两月产量的平均增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红爸爸上星期五买进某公司股票1000股,每股28元,星期六和星期天不交易.下表为本周内每日该股票的涨跌情况.(单位:元)

(1)通过上表你认为星期五收盘时,每股是多少元?
(2)本周内每股最高是多少?最低是多少元?
(3)已知股票买入时需交成交额1.5‰的交易费,卖出时需交成交额2.5‰的交易费.若星期五抛出,则小红爸爸这笔股票交易盈亏如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=10,BC=8,P为AD的中点,将△ABP沿BP翻折至△EBP(点A落到点E处),连接DE,则图中与∠APB相等的角的个数为( ) 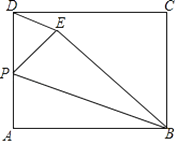
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,设正方体ABCD-A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从点A出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA1→A1D1→…,白甲壳虫爬行的路线是AB→BB1→…,并且都遵循如下规则:所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交(其中n是正整数),那么当黑、白两个甲壳虫各爬行完第2013条棱分别停止在所到的正方体顶点处时,它们之间的距离是 .
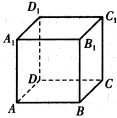
查看答案和解析>>
科目:初中数学 来源: 题型:
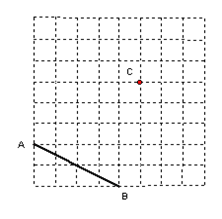
【题目】如图,在每个小正方形的边长都为1的方格纸上有线段AB和点C.
(1)画线段BC、画射线AC.
(2)过点C画直线AB的平行线EF.
(3)过点C画直线AB的垂线,垂足为点D.
(4)求△ABC的面积是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD、BC于E、F,作BH⊥AF于点H,分别交AC、CD于点G、P,连结GE、GF.
(1)求证:△OAE≌△OBG.
(2)试问:四边形BFGE是否为菱形?若是,请证明;若不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),过点P作PM∥CD交BC于M点,PN∥BC交CD于N点,连接MN,在运动过程中,则下列结论:
①△ABE≌△BCF;②AE=BF;③AE⊥BF;④CF2=PEBF;⑤线段MN的最小值为 ![]() .
.
其中正确的结论有( )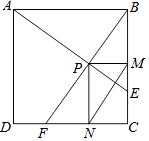
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com