
【题目】如图,在边长为1的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),过点P作PM∥CD交BC于M点,PN∥BC交CD于N点,连接MN,在运动过程中,则下列结论:
①△ABE≌△BCF;②AE=BF;③AE⊥BF;④CF2=PEBF;⑤线段MN的最小值为 ![]() .
.
其中正确的结论有( )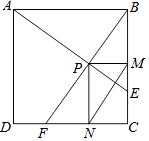
A.2个
B.3个
C.4个
D.5个
【答案】D
【解析】解:如图,
∵动点F,E的速度相同,
∴DF=CE,
又∵CD=BC,
∴CF=BE,
在△ABE和△BCF中,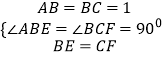
∴△ABE≌△BCF(SAS),故①正确;
∴∠BAE=∠CBF,AE=BF,故②正确;
∵∠BAE+∠BEA=90°,
∴∠CBF+∠BEA=90°,
∴∠APB=90°,故③正确;
在△BPE和△BCF中,
∵∠BPE=∠BCF,∠PBE=∠CBF,
∴△BPE∽△BCF,
∴ ![]() =
= ![]() ,
,
∴CFBE=PEBF,
∵CF=BE,
∴CF2=PEBF,故④正确;
∵点P在运动中保持∠APB=90°,
∴点P的路径是一段以AB为直径的弧,
设AB的中点为G,连接CG交弧于点P,此时CP的长度最小,
在Rt△BCG中,CG= ![]() =
= ![]() =
= ![]() ,
,
∵PG= ![]() AB=
AB= ![]() ,
,
∴CP=CG﹣PG= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
即线段CP的最小值为 ![]() ,故⑤正确;
,故⑤正确;
综上可知正确的有5个,
故选D.
由正方形的性质及条件可判断出①△ABE≌△BCF,即可判断出②AE=BF,∠BAE=∠CBF,再根据∠BAE+∠BEA=90°,可得∠CBF+∠BEA=90°,可得出∠APB=90°,即可判断③,由△BPE∽△BCF,利用相似三角形的性质,结合CF=BE可判断④;然后根据点P在运动中保持∠APB=90°,可得点P的路径是一段以AB为直径的弧,设AB的中点为G,连接CG交弧于点P,此时CP的长度最小,最后在Rt△BCG中,根据勾股定理,求出CG的长度,再求出PG的长度,即可求出线段CP的最小值,可判断⑤.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
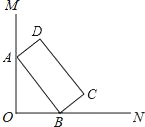
【题目】如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为( )
A. ![]() +1 B.
+1 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB表示路灯,当身高为1.6米的小名站在离路灯1.6的D处时,他测得自己在路灯下的影长DE与身高CD相等,当小明继续沿直线BD往前走到E点时,画出此时小明的影子,并计算此时小明的影长. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某地下商业街的入口,数学课外兴趣小组的同学打算运用所学的知识测量侧面支架的最高点E到地面的距离EF.经测量,支架的立柱BC与地面垂直,即∠BCA=90°,且BC=1.5m,点F,A,C在同一条水平线上,斜杆AB与水平线AC的夹角∠BAC=30°,支撑杆DE⊥AB于点D,该支架的边BE与AB的夹角∠EBD=60°,又测得AD=1m.请你求出该支架的边BE及顶端E到地面的距离EF的长度. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,AB∥DE,AF∥DC,E、F两点在BC上,且四边形AEFD是平行四边形.
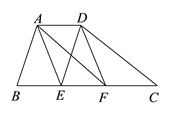
(1)AD与BC有何等量关系?请说明理由;
(2)当AB=DC时,求证:四边形AEFD是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠BAC=90°,AD⊥BC于D,则下列结论中,正确的个数为( )
①AB⊥AC;②AD与AC互相垂直;③点C到AB的垂线段是线段AB;④点A到BC的距离是线段AD的长度;⑤线段AB的长度是点B到AC的距离;⑥线段AB是点B到AC的距离;

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现从A,B向甲、乙两地运送蔬菜,A,B两个蔬菜市场各有蔬菜14吨,其中甲地需要蔬菜15吨,乙地需要蔬菜13吨,从A到甲地运费50元/吨,到乙地30元/吨;从B地到甲运费60元/吨,到乙地45元/吨.
(1)设A地到甲地运送蔬菜x吨,请完成下表:
运往甲地(单位:吨) | 运往乙地(单位:吨) | |
A | x | |
B |
(2)设总运费为W元,请写出W与x的函数关系式
(3)怎样调运蔬菜才能使运费最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D、E在AB上,且D、E分别是AC、BC的垂直平分线上一点;若△CDE的周长为4,则AB的长为___________;若∠ACB=100°,则∠DCE=_________度; 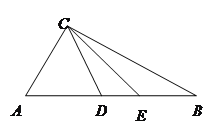
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com