
【题目】如图,小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为60°和35°,已知大桥BC的长度为100m,且与地面在同一水平面上.求热气球离地面的高度. (结果保留整数,参考数据:sin35°≈ ![]() ,cos35°≈
,cos35°≈ ![]() ,tan35°≈
,tan35°≈ ![]() ,
, ![]() ≈1.7)
≈1.7)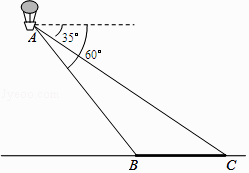
【答案】解:作AD⊥CB交CB所在直线于点D,由题知, ∠ACD=35°,∠ABD=60°,
∵在Rt△ACD中,∠ACD=35°,tan35°= ![]() ≈
≈ ![]() ,
,
∴CD= ![]() AD.
AD.
∵在Rt△ABD中,∠ABD=60°,tan60°= ![]() =
= ![]() ≈1.7,
≈1.7,
∴BD= ![]() AD,
AD,
∴BC=CD﹣BD= ![]() AD﹣
AD﹣ ![]() AD,
AD,
∴ ![]() AD﹣
AD﹣ ![]() AD=100,解得AD=119m.
AD=100,解得AD=119m.
答:热气球离地面的高119m.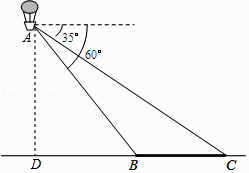
【解析】作AD⊥CB交CB所在直线于点D,利用锐角三角函数的定义求出CD及BD的长,利用BC=CD﹣BD即可得出结论.
【考点精析】利用关于仰角俯角问题对题目进行判断即可得到答案,需要熟知仰角:视线在水平线上方的角;俯角:视线在水平线下方的角.


科目:初中数学 来源: 题型:
【题目】有下列四个条件:①AB=BC,②∠ABC=90![]() ,③AC=BD,④AC⊥BD.从中选取两个作为补充条件,使□BCD为正方形(如图).现有下列四种选法,其中错误的是 ( )
,③AC=BD,④AC⊥BD.从中选取两个作为补充条件,使□BCD为正方形(如图).现有下列四种选法,其中错误的是 ( )
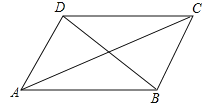
A. ②③ B. ②④ C. ①② D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=10,BC=8,P为AD的中点,将△ABP沿BP翻折至△EBP(点A落到点E处),连接DE,则图中与∠APB相等的角的个数为( ) 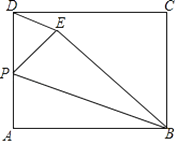
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,设正方体ABCD-A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从点A出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA1→A1D1→…,白甲壳虫爬行的路线是AB→BB1→…,并且都遵循如下规则:所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交(其中n是正整数),那么当黑、白两个甲壳虫各爬行完第2013条棱分别停止在所到的正方体顶点处时,它们之间的距离是 .
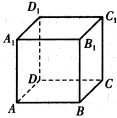
查看答案和解析>>
科目:初中数学 来源: 题型:
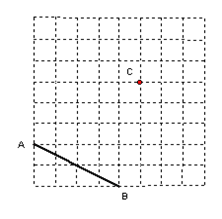
【题目】如图,在每个小正方形的边长都为1的方格纸上有线段AB和点C.
(1)画线段BC、画射线AC.
(2)过点C画直线AB的平行线EF.
(3)过点C画直线AB的垂线,垂足为点D.
(4)求△ABC的面积是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】生态公园计划在园内的坡地上种植一片有A、B两种树的混合林,需要购买这两种树苗共100棵.假设这批树苗种植后成活95棵,种植A、B两种树苗的相关信息如下表:

(1)求购买这两种树苗各多少棵?
(2)求种植这片混合林的总费用需多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD、BC于E、F,作BH⊥AF于点H,分别交AC、CD于点G、P,连结GE、GF.
(1)求证:△OAE≌△OBG.
(2)试问:四边形BFGE是否为菱形?若是,请证明;若不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种新运算⊙:1⊙3=1×4+3=7; 3⊙(-1)=3×4-1=11;(-5)⊙4=(-5)×4+4=-16; (-4)⊙(-3)=(-4)×4-3=-19.
(1)由以上式子可知:a⊙b= ;
(2)若a⊙(-2b)=4,请计算(a-b)⊙(2a+b)的值;
(3)若[x⊙(-2)] ⊙ [(-x)⊙2]=6,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(5,0)两点,直线y=﹣ ![]() x+3与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
x+3与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.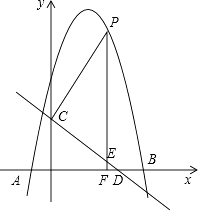
(1)求抛物线的解析式;
(2)若PE=5EF,求m的值;
(3)若点E′是点E关于直线PC的对称点,是否存在点P,使点E′落在y轴上?若存在,请直接写出相应的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com