
【题目】已知正比例函数y=k1x的图象与反比例函数y= ![]() 的图象的一个交点是(2,3).
的图象的一个交点是(2,3).
(1)求出这两个函数的表达式;
(2)作出两个函数的草图,利用你所作的图形,猜想并验证这两个函数图象的另一个交点的坐标;
(3)直接写出使反比例函数值大于正比例函数值的x的取值范围.
科目:初中数学 来源: 题型:
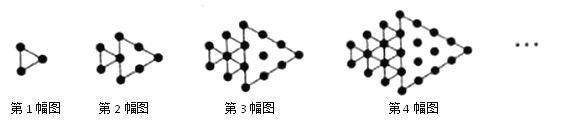
【题目】如图所示,将形状、大小完全相同的“![]() ”和线段按照一定规律摆成下列图形.第1幅图形中“
”和线段按照一定规律摆成下列图形.第1幅图形中“![]() ”的个数为
”的个数为![]() ,第2幅图形中“
,第2幅图形中“![]() ”的个数为
”的个数为![]() ,第3幅图形中“
,第3幅图形中“![]() ”的个数为
”的个数为![]() ,……,以此类推,解决以下问题:
,……,以此类推,解决以下问题:
(1)直接写出![]() ,
,![]() (用含n的代数式表示);
(用含n的代数式表示);
(2)猜想是否存在某幅图中“![]() ”的个数为2018,若存在,直接写出n的值;若不存在,则直接写出2018至少再加上多少后所得的数正好是某幅图中黑点的个数,并直接写出此时n的值;
”的个数为2018,若存在,直接写出n的值;若不存在,则直接写出2018至少再加上多少后所得的数正好是某幅图中黑点的个数,并直接写出此时n的值;
(3)求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB表示路灯,当身高为1.6米的小名站在离路灯1.6的D处时,他测得自己在路灯下的影长DE与身高CD相等,当小明继续沿直线BD往前走到E点时,画出此时小明的影子,并计算此时小明的影长. 
查看答案和解析>>
科目:初中数学 来源: 题型:
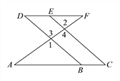
【题目】如图,E点为DF上的点,B为AC上的点,![]() ,
,![]() ,求证:DF∥AC.
,求证:DF∥AC.
证明:∵ ![]() (已知),∠1=∠3,∠2=∠4( ),
(已知),∠1=∠3,∠2=∠4( ),
∴∠3=∠4(等量代换).
∴__________![]() __________( ).
__________( ).
∴∠C=∠ABD( ).
∵∠C=∠D( ),
∴∠D=__________( ).
∴AC∥DF( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,AB∥DE,AF∥DC,E、F两点在BC上,且四边形AEFD是平行四边形.
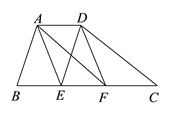
(1)AD与BC有何等量关系?请说明理由;
(2)当AB=DC时,求证:四边形AEFD是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
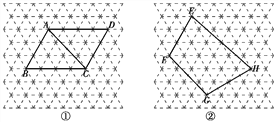
【题目】图中的虚线网格是等边三角形网格,它的每一个小三角形都是边长为1的等边三角形.
(1)边长为1的等边三角形的高=____;
(2)图①中的ABCD的对角线AC的长=____;
(3)图②中的四边形EFGH的面积=____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,B在x轴上,四边形OACB为平行四边形,且∠AOB=60°,反比例函数![]() (k>0)在第一象限内过点A,且与BC交于点F.(1)若OA=10,求反比例函数的解析式;
(k>0)在第一象限内过点A,且与BC交于点F.(1)若OA=10,求反比例函数的解析式;
(2)若F为BC的中点,且S△AOF=24![]() ,求OA长及点C坐标;
,求OA长及点C坐标;
(3)在(2)的条件下,过点F作EF∥OB交OA于点E(如图2),若点P是直线EF上一个动点,连结,PA,PO,问是否存在点P,使得以P,A,O三点构成的三角形是直角三角形?若存在,请指出这样的P点有几个,并直接写出其中二个P点坐标;若不存在,请说明了理由.
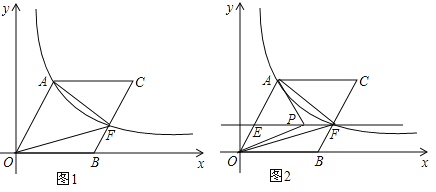
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com