
【题目】如图1,将△ABC纸片沿中位线EH折叠,使点A对称点D落在BC边上,再将纸片分别沿等腰△BED和等腰△DHC的底边上的高线EF,HG折叠,折叠后的三个三角形拼合形成一个矩形,类似地,对多边形进行折叠,若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩形,这样的矩形称为叠合矩形.




(1)将□ABCD纸片按图2的方式折叠成一个叠合矩形AEFG,则操作形成的折痕分别是线段_______,_________;S矩形AEFG:S□ABCD=__________.
(2)□ABCD纸片还可以按图3的方式折叠成一个叠合矩形EFGH,若EF=5,EH=12,求AD的长;
(3)如图4,四边形ABCD纸片满足AD∥BC,AD<BC,AB⊥BC,AB=8,CD=10,小明把该纸片折叠,得到叠合正方形,请你帮助画出一种叠合正方形的示意图,并求出AD、BC的长.
【答案】 AE GF 1:2
【解析】分析:(1)由图可直接得到第一、二空答案,根据折叠的性质可得△AEH与△ABE面积相等、梯形HFGA与梯形FCDG面积相等,据此不难得到第三空答案;
(2)对图形进行点标注,如图所示:首先根据勾股定理求得FH的长,再根据折叠的性质以及请到的知识可得AH=FN,HD=HN,然后根据线段和差关系即可得到AD的长;
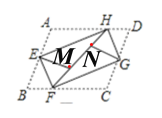
(3)根据题目信息,动手这一下,然后将结合画出来,再结合折叠的性质以及勾股定理的知识分析解答即可.
详解:(1)根据题意得:操作形成的折痕分别是线段AE、GF;
由折叠的性质得:△ABE≌△AHE,四边形AHFG≌四边形DCFG,
∴△ABE的面积=△AHE的面积,四边形AHFG的面积=四边形DCFG的面积,
∴S矩形AEFG=![]() S平行四边形ABCD,
S平行四边形ABCD,
∴S矩形AEFG:S平行四边形ABCD=1:2;
故答案为:AE,GF,1:2;
(2)∵四边形EFGH是矩形,
∴∠HEF=90°,
∴FH=![]() =13,
=13,
由折叠的性质得:AD=FH=13;
由折叠的对称性可知:DH=NH,AH=HM,CF=FN.
易得△AEH≌CGF,
所以CF=AH,
所以AD=DH+AH=HN+FN=FH=13.

(3)有3种折法,如图4、图5、图6所示:
①折法1中,如图4所示:
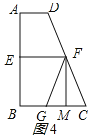
由折叠的性质得:AD=BG,AE=BE=![]() AB=4,CF=DF=
AB=4,CF=DF=![]() CD=5,GM=CM,∠FMC=90°,
CD=5,GM=CM,∠FMC=90°,
∵四边形EFMB是叠合正方形,
∴BM=FM=4,
∴GM=CM=![]() =3,
=3,
∴AD=BG=BM-GM=1,BC=BM+CM=7;
②折法2中,如图5所示:
由折叠的性质得:四边形EMHG的面积=![]() 梯形ABCD的面积,AE=BE=
梯形ABCD的面积,AE=BE=![]() AB=4,DG=NG,NH=CH,BM=FM,MN=MC,
AB=4,DG=NG,NH=CH,BM=FM,MN=MC,
∴GH=![]() CD=5,
CD=5,
∵四边形EMHG是叠合正方形,
∴EM=GH=5,正方形EMHG的面积=52=25,
∵∠B=90°,
∴FM=BM=![]() =3,
=3,
设AD=x,则MN=FM+FN=3+x,
∵梯形ABCD的面积=![]() (AD+BC)×8=2×25,
(AD+BC)×8=2×25,
∴AD+BC=![]() ,
,
∴BC=![]() -x,
-x,
∴MC=BC-BM=![]() -x-3,
-x-3,
∵MN=MC,
∴3+x=![]() -x-3,
-x-3,
解得:x=![]() ,
,
∴AD=![]() ,BC=
,BC=![]() -
-![]() =
=![]() ;
;
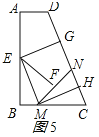
③折法3中,如图6所示,作GM⊥BC于M,
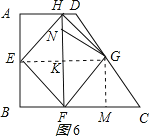
则E、G分别为AB、CD的中点,
则AH=AE=BE=BF=4,CG=![]() CD=5,正方形的边长EF=GF=4
CD=5,正方形的边长EF=GF=4![]() ,
,
GM=FM=4,CM=![]() =3,
=3,
∴BC=BF+FM+CM=11,FN=CF=7,DH=NH=8-7=1,
∴AD=5.


 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
【题目】 如图,已知△ABC,AB=AC=1,∠A=36°,∠ABC的平分线BD交AC于点D,则AD的长是 , cosA的值是 . (结果保留根号) 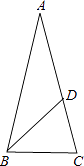
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商店只有雪碧、可乐、果汁、奶汁四种饮料,每种饮料数量充足,某同学去该店购买饮料,每种饮料被选中的可能性相同.
(1)若他去买一瓶饮料,则他买到奶汁的概率是;
(2)若他两次去买饮料,每次买一瓶,且两次所买饮料品种不同,请用树状图或列表法求出他恰好买到雪碧和奶油的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点,连接MP,MQ,PQ.在整个运动过程中,△MPQ的面积大小变化情况是( )
A.一直增大
B.一直减小
C.先减小后增大
D.先增大后减少
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了节约用水,对自来水的收费标准作如下规定:每月每户用水不超过10吨的部分,按2元/吨收费;超过10吨的部分按2.5元/吨收费.
(1)若黄老师家5月份用水16吨,问应交水费多少元?
(2)若黄老师家6月份交水费30元,问黄老师家5月份用水多少吨?
(3)若黄老师家7月用水a吨,问应交水费多少元?(用a的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两条轮船同时从港口A出发,甲轮船以每小时30海里的速度沿着北偏东60°的方向航行,乙轮船以每小时15海里的速度沿着正东方向行进,1小时后,甲船接到命令要与乙船会合,于是甲船改变了行进的速度,沿着东南方向航行,结果在小岛C处与乙船相遇.假设乙船的速度和航向保持不变,求:
(1)港口A与小岛C之间的距离;
(2)甲轮船后来的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名射击运动员中进行射击比赛,两人在相同条件下各射击10次,射击的成绩如图所示.

根据图中信息,回答下列问题:
(1)甲的平均数是___________,乙的中位数是______________;
(2)分别计算甲、乙成绩的方差,并从计算结果来分析,你认为哪位运动员的射击成绩更稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
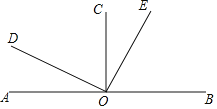
【题目】如图,已知直线AB上一点O,OC⊥AB,OD⊥OE, 若∠COE=![]() ∠BOD.
∠BOD.
(1)求∠COE, ∠BOD, ∠AOE的度数.
(2)若OF平分∠BOE,求∠AOF的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com