
【题目】甲、乙两名射击运动员中进行射击比赛,两人在相同条件下各射击10次,射击的成绩如图所示.

根据图中信息,回答下列问题:
(1)甲的平均数是___________,乙的中位数是______________;
(2)分别计算甲、乙成绩的方差,并从计算结果来分析,你认为哪位运动员的射击成绩更稳定?
【答案】(1)8,7.5 ;(2)乙运动员的射击成绩更稳定.
【解析】
试题分析:(1)求甲的平均数只要把甲的十次射击成绩加在一起除以10即可;求乙的中位数先把乙的十次射击成绩按从小到大顺序排列,则排在中间两个数据的平均数就是乙的中位数;(2)先计算出甲,乙的平均数,根据方差计算公式(各个数据与平均数差的平方和再除以10),即可算出两位运动员的方差,谁的方差小,谁的成绩就稳定.
试题解析:(1)把甲的十次射击成绩加在一起除以10:甲的平均数=(6+10+8+9+8+7+8+10+7+7)÷10=8;先把乙的十次射击成绩按从小到大顺序排列为7,7,7,7,7,8,9,9,9,10.则排在中间两个数据是7,8.故乙的中位数是(7+8)÷2=7.5;(2)甲的平均数是8,乙的平均数是(7+7+7+7+7+8+9+9+9+10)÷10=8,故![]()
![]() ,
,![]() =
=![]() ,
,![]() ,∴乙运动员的射击成绩更稳定.
,∴乙运动员的射击成绩更稳定.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M,N分别在AB,AD边上,若AM:MB=AN:ND=1:2,则sin∠MCN=( ) 
A.![]()
B.![]()
C.![]()
D.![]() ﹣2
﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将△ABC纸片沿中位线EH折叠,使点A对称点D落在BC边上,再将纸片分别沿等腰△BED和等腰△DHC的底边上的高线EF,HG折叠,折叠后的三个三角形拼合形成一个矩形,类似地,对多边形进行折叠,若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩形,这样的矩形称为叠合矩形.




(1)将□ABCD纸片按图2的方式折叠成一个叠合矩形AEFG,则操作形成的折痕分别是线段_______,_________;S矩形AEFG:S□ABCD=__________.
(2)□ABCD纸片还可以按图3的方式折叠成一个叠合矩形EFGH,若EF=5,EH=12,求AD的长;
(3)如图4,四边形ABCD纸片满足AD∥BC,AD<BC,AB⊥BC,AB=8,CD=10,小明把该纸片折叠,得到叠合正方形,请你帮助画出一种叠合正方形的示意图,并求出AD、BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明新家装修,在装修客厅时,购进彩色地砖和单色地砖共100块,共花费5600元.已知彩色地砖的单价是80元/块,单色地砖的单价是40元/块.
(1)两种型号的地砖各采购了多少块?
(2)如果厨房也要铺设这两种型号的地砖共60块,且采购地砖的费用不超过3200元,那么彩色地砖最多能采购多少块?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车间的甲、乙两名工人分别同时生产500只同一型号的零件,他们生产的零件y(只)与生产时间x(分)的函数关系的图象如图所示.根据图象提供的信息解答下列问题: 
(1)甲每分钟生产零件只;乙在提高生产速度之前已生产了零件 只;
(2)若乙提高速度后,乙的生产速度是甲的2倍,请分别求出甲、乙两人生产全过程中,生产的零件y(只)与生产时间x(分)的函数关系式;
(3)当两人生产零件的只数相等时,求生产的时间;并求出此时甲工人还有多少只零件没有生产.
查看答案和解析>>
科目:初中数学 来源: 题型:
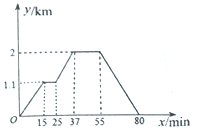
【题目】如图,反映的过程是小涛从家出发,去菜地浇水,又去玉米地锄草,然后回家.其中x表示时间,y表示小涛离家的距离.
(1)菜地离小涛家的距离是____km,小涛走到菜地用了____min,小涛给菜地浇水用了___min.
(2)菜地离玉米地的距离是____km,小涛从菜地到地用了____min,小涛给玉米地锄草用了____min.
(3)玉米地离小涛家的距离是___km,小涛从玉米地走回家的平均速度是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,以大于![]() BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,得四边形ABEF.
BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,得四边形ABEF.
求证:四边形ABEF是菱形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com