
【题目】如图,已知ABCD的顶点A、C分别在直线x=2和x=5上,O是坐标原点,则对角线OB长的最小值为 . 
【答案】7
【解析】解:过点B作BD⊥直线x=5,交直线x=5于点D,过点B作BE⊥x轴,交x轴于点E,直线x=2与OC交于点M,与x轴交于点F,直线x=5与AB交于点N,如图: ∵四边形OABC是平行四边形,
∴∠OAB=∠BCO,OC∥AB,OA=BC,
∵直线x=2与直线x=5均垂直于x轴,
∴AM∥CN,
∴四边形ANCM是平行四边形,
∴∠MAN=∠NCM,
∴∠OAF=∠BCD,
∵∠OFA=∠BDC=90°,
∴∠FOA=∠DBC,
在△OAF和△BCD中, ,
,
∴△OAF≌△BCD(ASA).
∴BD=OF=2,
∴OE=5+2=7,
∴OB= ![]() .
.
由于OE的长不变,所以当BE最小时(即B点在x轴上),OB取得最小值,最小值为OB=OE=7.
故答案为:7.
过点B作BD⊥直线x=5,交直线x=5于点D,过点B作BE⊥x轴,交x轴于点E.则由勾股定理可求出OB的长.由于四边形OABC是平行四边形,所以OA=BC,又由平行四边形的性质可推得∠OAF=∠BCD,则可证明△OAF≌△BCD,所以OE的长固定不变,当BE最小时,OB取得最小值,从而可求.


科目:初中数学 来源: 题型:
【题目】设a1 , a2 , …,a2017是从1,0,﹣1这三个数中取值的一列数,若a1+a2+…+a2017=84,(a1+1)2+(a2+1)2+…+(a2017+1)2=4001,则a1 , a2 , …,a2017中为0的个数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了节约用水,对自来水的收费标准作如下规定:每月每户用水不超过10吨的部分,按2元/吨收费;超过10吨的部分按2.5元/吨收费.
(1)若黄老师家5月份用水16吨,问应交水费多少元?
(2)若黄老师家6月份交水费30元,问黄老师家5月份用水多少吨?
(3)若黄老师家7月用水a吨,问应交水费多少元?(用a的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示中的几个图形是五角星和它的变形.
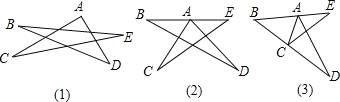
![]() 图甲中是一个五角星形状,求证:
图甲中是一个五角星形状,求证:![]() ;
;
![]() 图甲中的点A向下移到BE上时
图甲中的点A向下移到BE上时![]() 如图乙
如图乙![]() 五个角的和
五个角的和![]() 即
即![]() 有无变化?试说明理由
有无变化?试说明理由
![]() 把图乙中的点C向上移动到BD上时
把图乙中的点C向上移动到BD上时![]() 如图丙所示
如图丙所示![]() ,五个角的和
,五个角的和![]() 即
即![]() 有无变化?试说明理由.
有无变化?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名射击运动员中进行射击比赛,两人在相同条件下各射击10次,射击的成绩如图所示.

根据图中信息,回答下列问题:
(1)甲的平均数是___________,乙的中位数是______________;
(2)分别计算甲、乙成绩的方差,并从计算结果来分析,你认为哪位运动员的射击成绩更稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
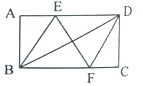
【题目】如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD.若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为 ( )
A. ![]() B. 2
B. 2![]() C. 3
C. 3![]() D. 6
D. 6![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年G20杭州峰会期间,某志愿者小组有五名翻译,其中一名只会翻译法语,三名只会翻译英语,还有一名两种语言都会翻译.若从中随机挑选两名组成一组,则该组能够翻译上述两种语言的概率是多少?(请用“画树状图”的方法给出分析过程,并求出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上的任意一点 (不与点A、B重合),连接CO并延长CO交⊙O于点D,连接AD. 
(1)弦长AB等于(结果保留根号);
(2)当∠D=20°时,求∠BOD的度数;
(3)当AC的长度为多少时,以A、C、D为顶点的三角形与以B、C、0为顶点的三角形相似?请写出解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于O,OE⊥AB,OF⊥CD。
(1)图中与∠COE互补的角是___________________; (把符合条件的角都写出来)
(2)如果∠AOC =![]() ∠EOF ,求∠AOC的度数。
∠EOF ,求∠AOC的度数。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com