
【题目】利用平方根去根号可以构造一个整系数方程.例如:x= ![]() +1时,移项得x﹣1=
+1时,移项得x﹣1= ![]() ,两边平方得(x﹣1)2=(
,两边平方得(x﹣1)2=( ![]() )2 , 所以x2﹣2x+1=2,即x2﹣2x﹣1=0.仿照上述构造方法,当x=
)2 , 所以x2﹣2x+1=2,即x2﹣2x﹣1=0.仿照上述构造方法,当x= ![]() 时,可以构造出一个整系数方程是( )
时,可以构造出一个整系数方程是( )
A.4x2+4x+5=0
B.4x2+4x﹣5=0
C.x2+x+1=0
D.x2+x﹣1=0
科目:初中数学 来源: 题型:
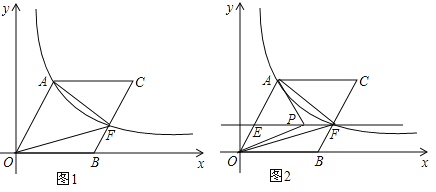
【题目】在平面直角坐标系中,O为坐标原点,B在x轴上,四边形OACB为平行四边形,且∠AOB=60°,反比例函数![]() (k>0)在第一象限内过点A,且与BC交于点F.(1)若OA=10,求反比例函数的解析式;
(k>0)在第一象限内过点A,且与BC交于点F.(1)若OA=10,求反比例函数的解析式;
(2)若F为BC的中点,且S△AOF=24![]() ,求OA长及点C坐标;
,求OA长及点C坐标;
(3)在(2)的条件下,过点F作EF∥OB交OA于点E(如图2),若点P是直线EF上一个动点,连结,PA,PO,问是否存在点P,使得以P,A,O三点构成的三角形是直角三角形?若存在,请指出这样的P点有几个,并直接写出其中二个P点坐标;若不存在,请说明了理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
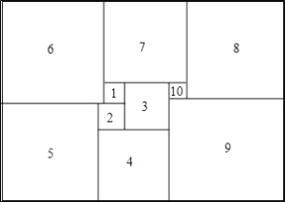
【题目】如图所示,1925年数学家莫伦发现的世界上第一个完美长方形,它恰能被分割成10个大小不同的正方形.若标注①、②的正方形边长分别为5和6,请你直接写出以下数据:
(1)第6个正方形的边长= ;
(2)第8个正方形的边长= ;
(3)整个长方形的面积= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为疏导国庆假期交通,一辆交通巡逻车在南北公路上巡视.某天早上从![]() 地出发,中午到达
地出发,中午到达![]() 地,行驶记录如下(规定向北为正方向,单位:千米):
地,行驶记录如下(规定向北为正方向,单位:千米):
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
请你解答下列问题:
(1)![]() 地在
地在![]() 地的什么方向?与
地的什么方向?与![]() 地相距多远?
地相距多远?
(2)巡逻车在巡逻中,离开![]() 地最远多少千米?
地最远多少千米?
(3)若巡逻车行驶每千米耗油![]() 升,这半天共耗油多少升?
升,这半天共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,我们不妨将横坐标,纵坐标均为整数的点称之为“中国结”.
(1)求函数y= ![]() x+2的图象上所有“中国结”的坐标;
x+2的图象上所有“中国结”的坐标;
(2)若函数y= ![]() (k≠0,k为常数)的图象上有且只有两个“中国结”,试求出常数k的值与相应“中国结”的坐标;
(k≠0,k为常数)的图象上有且只有两个“中国结”,试求出常数k的值与相应“中国结”的坐标;
(3)若二次函数y=(k2﹣3k+2)x2+(2k2﹣4k+1)x+k2﹣k(k为常数)的图象与x轴相交得到两个不同的“中国结”,试问该函数的图象与x轴所围成的平面图形中(含边界),一共包含有多少个“中国结”?
查看答案和解析>>
科目:初中数学 来源: 题型:
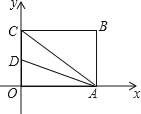
【题目】如图,四边形OABC为矩形,点A,C分别在x轴和y轴上,连接AC,点B的坐标为(8,6),∠CAO的平分线与y轴相交于点D,则点D的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于O点,且BE=BF,∠BEF=2∠BAC。

(1)求证:OE=OF;
(2)若BC=![]() ,求AB的长。
,求AB的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,在Rt ΔABC中,∠ABC=900, AB=BC=2.
(1)用尺规作∠A的平分线AD.
(2)角平分线AD交BC于点D,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
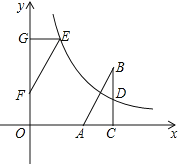
【题目】如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上,∠ACB=90°,AC=1,反比例函数![]() (k>0)的图象经过BC边的中点D(3,1).
(k>0)的图象经过BC边的中点D(3,1).
(1)求这个反比例函数的表达式;
(2)若△ABC与△EFG成中心对称,且△EFG的边FG在y轴的正半轴上,点E在这个函数的图象上.
①求OF的长;
②连接AF,BE,证明四边形ABEF是正方形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com