
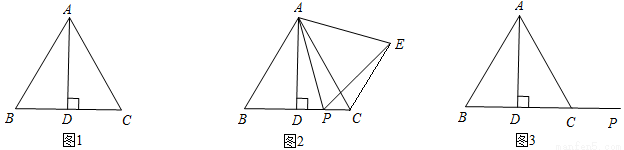
在等边三角形ABC中,AD⊥BC于点D.
(1)如图1,请你直接写出线段AD与BC之间的数量关系: AD= BC ;
(2)如图2,若P是线段BC上一个动点(点P不与点B、C重合),联结AP,将线段AP绕点A逆时针旋转60°,得到线段AE,联结CE,猜想线段AD、CE、PC之间的数量关系,并证明你的结论;
(3)如图3,若点P是线段BC延长线上一个动点,(2)中的其他条件不变,按照(2)中的作法,请在图3中补全图形,并直接写出线段AD、CE、PC之间的数量关系.
(1)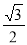 ;(2)AD=
;(2)AD=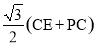 ,理由见解析;(3)补图见解析,AD=
,理由见解析;(3)补图见解析,AD=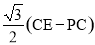 .
.
【解析】
试题分析:(1)根据等边三角形的性质,得∠B=600,AB=BC,所以根据锐角三角函数定义和特殊角的三角函数值求得AD=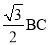 .
.
(2)根据等边三角形和旋转的性质,证明△ABP≌△ACE即可求得结论.
(3)类同(2)的证明.
试题解析:(1)∵等边三角形ABC,∴∠B=600,AB=BC.
又∵AD⊥BC,∴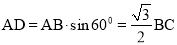 .
.
(2)AD=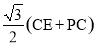 .理由如下:
.理由如下:
∵线段AP绕点A逆时针旋转60°,得到线段AE,∴∠PAE=60°,AP=AE.
∵等边三角形ABC,∴∠BAC=60°,AB=AC.
∴∠BAC﹣∠PAC=∠PAE﹣∠PAC.∴∠BAP=∠CAE.
在△ABP和△ACE中,∵ ,
,
∴△ABP≌△ACE.∴BP=CE.
∵BP+PC=BC,∴CE+ PC=BC.
∵AD=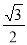 BC,∴AD=
BC,∴AD=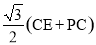 .
.
(3)补全图形如图:
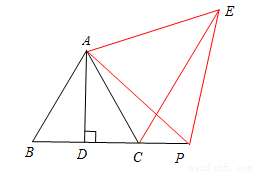
∵线段AP绕点A逆时针旋转60°,得到线段AE,∴∠PAE=60°,AP=AE.
∵等边三角形ABC,∴∠BAC=60°,AB=AC.
∴∠BAC+∠PAC=∠PAE+∠PAC.∴∠BAP=∠CAE.
在△ABP和△ACE中,∵ ,
,
∴△ABP≌△ACE.∴BP=CE.
∵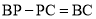 ,∴
,∴ .
.
∵AD=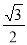 BC,∴AD=
BC,∴AD=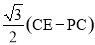 .
.
考点:1.线动旋转问题;2.等边三角形的性质;3.全等三角形的判定和性质;4.锐角三角函数定义;5.特殊角的三角函数值.


科目:初中数学 来源:2013-2014学年北京市昌平区中考一模数学试卷(解析版) 题型:填空题
如图,已知平行四边形纸片ABCD的周长为20,将纸片沿某条直线折叠,使点D与点B重合,折痕交AD于点E,交BC于点F,连接BE,则△ABE的周长为 .

查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市昌平区中考一模数学试卷(解析版) 题型:选择题
如图,已知AB∥CD,EA是∠CEB的平分线,若∠BED=40°,则∠A的度数是( )

A.40° B.50° C.70° D.80°
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市大兴区中考一模数学试卷(解析版) 题型:解答题
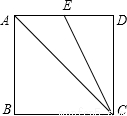
已知:如图,正方形ABCD中,点E为AD边的中点,联结CE.
求cos∠ACE和tan∠ACE的值.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市大兴区中考一模数学试卷(解析版) 题型:填空题
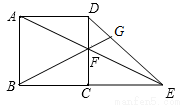
已知正方形ABCD的边长为2,E为BC边的延长线上一点,CE=2,联结AE,与CD交于点F,联结BF并延长与线段DE交于点G,则BG的长为 .
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市丰台区中考二模数学卷(解析版) 题型:解答题
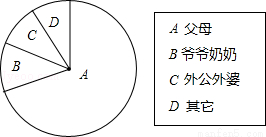
某市在2013年义务教育质量监测过程中,为了解学生的家庭教育情况,就八年级学生平时主要和谁在一起生活进行了抽样调查.下面是根据这次调查情况制作的不完整的频数分布表和扇形统计图.
频数分布表
代码和谁一起生活频数频率
A父母42000.7
B爷爷奶奶660a
C外公外婆6000.1
D其它b0.09
合计60001
请根据上述信息,回答下列问题:
(1)a= ,b= ;
(2)在扇形统计图中,和外公外婆一起生活的学生所对应扇形圆心角的度数是 ;
(3)若该市八年级学生共有3万人,估计不与父母一起生活的学生有 人.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年内蒙古满洲里市九年级三月月考数学试卷(解析版) 题型:选择题
生物具有遗传多样性,遗传信息大多储存在DNA分子上.一个DNA分子的直径约为0.0000002 ,这个数量用科学记数法可表示为 ( )
A. 0.2×10—6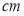 B. 2×10—6
B. 2×10—6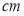 C. 0.2×10—7
C. 0.2×10—7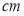 D. 2×10—7
D. 2×10—7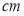
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.30° | B.36° | C.40° | D.45° |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com