
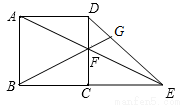
已知正方形ABCD的边长为2,E为BC边的延长线上一点,CE=2,联结AE,与CD交于点F,联结BF并延长与线段DE交于点G,则BG的长为 .
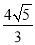 .
.
【解析】
试题分析:利用全等三角形的判定AAS得出△ADF≌△ECF,进而得出FG是△DCP的中位线,得出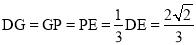 ,再利用勾股定理得出BG的长即可:
,再利用勾股定理得出BG的长即可:
如图,过点C作CP∥BG,交DE于点P.
∵BC=CE=2,∴CP是△BEG的中位线.∴P为EG的中点.
又∵AD=CE=1,AD∥CE,
∴在△ADF和△ECF中,∠AFD=∠EFC,∠ADC=∠FCE,AD=CE,
∴△ADF≌△ECF(AAS).∴CF=DF.
又CP∥FG,∴FG是△DCP的中位线.∴G为DP的中点.
∵CD=CE=2,∴DE=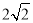 .
.
∴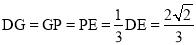 .
.
连接BD,
易知∠BDC=∠EDC=45°,∴∠BDE=90°.
又∵BD=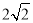
∴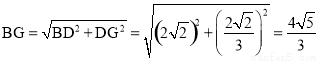 .
.
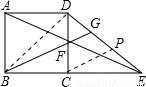
考点:1.正方形的性质;2.全等三角形的判定和性质;3.勾股定理;4.三角形中位线定理.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2013-2014学年北京市大兴区中考一模数学试卷(解析版) 题型:解答题
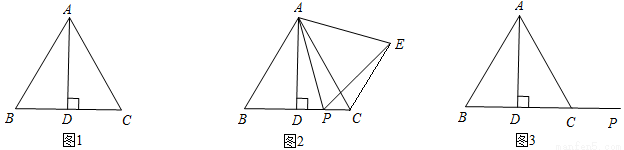
在等边三角形ABC中,AD⊥BC于点D.
(1)如图1,请你直接写出线段AD与BC之间的数量关系: AD= BC ;
(2)如图2,若P是线段BC上一个动点(点P不与点B、C重合),联结AP,将线段AP绕点A逆时针旋转60°,得到线段AE,联结CE,猜想线段AD、CE、PC之间的数量关系,并证明你的结论;
(3)如图3,若点P是线段BC延长线上一个动点,(2)中的其他条件不变,按照(2)中的作法,请在图3中补全图形,并直接写出线段AD、CE、PC之间的数量关系.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市大兴区中考一模数学试卷(解析版) 题型:解答题
在平面直角坐标系xOy中,直线l与直线 y= -2x关于y轴对称,直线l与反比例函数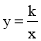 的图象的一个交点为A(2, m).
的图象的一个交点为A(2, m).
(1)试确定反比例函数的表达式;
(2)若过点A的直线与x轴交于点B,且∠ABO=45°,直接写出点B的坐标.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市大兴区中考一模数学试卷(解析版) 题型:选择题
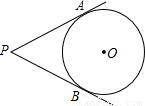
已知:如图,PA切⊙O于点A,PB切⊙O于点B,如果∠APB=60°,⊙O半径是3,则劣弧AB的长为( )
A.π B.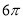 C.2π D.3π
C.2π D.3π
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市丰台区中考二模数学卷(解析版) 题型:解答题
如图,经过原点的抛物线y=-x2+bx(b>2)与x轴的另一交点为A,过点P(1,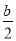 )作直线PN⊥x轴于点N,交抛物线于点B.点B关于抛物线对称轴的对称点为C.连结CB,CP.
)作直线PN⊥x轴于点N,交抛物线于点B.点B关于抛物线对称轴的对称点为C.连结CB,CP.
(1)当b=4时,求点A的坐标及BC的长;
(2)连结CA,求b的适当的值,使得CA⊥CP;
(3)当b=6时,如图2,将△CBP绕着点C按逆时针方向旋转,得到△CB′P′,CP与抛物线对称轴的交点为E,点M为线段B′P′(包含端点)上任意一点,请直接写出线段EM长度的取值范围.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市丰台区中考二模数学卷(解析版) 题型:选择题
如图,正方形ABCD的边长为2cm,在对称中心O处有一个钉子.动点P、Q同时从点A出发,点P沿A-B-C方向以每秒2cm的速度运动,到C点停止,点Q沿A-D方向以每秒1cm的速度运动,到D点停止.PQ两点用一条可伸缩的细橡皮筋联结,当遇到钉子后,橡皮筋会自动弯折.如果x秒后橡皮筋扫过的面积为ycm2,那么y与x的函数关系图象可能是( )

A.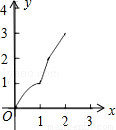 B.
B.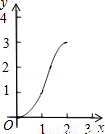 C.
C.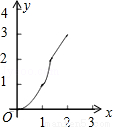 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com