①②
分析:根据等边三角形的性质推出AD=AB,AE=AC,∠ADB=∠ABD=60°,∠DAB=∠EAC=60°,求出∠DAC=∠BAE,根据SAS证△DAC≌△BAE,推出BE=DC,∠ADC=∠ABE,根据三角形的内角和定理求出∠BOD=180°-∠ODB-∠DBA-∠ABE=60°,根据等边三角形性质得出∠ADB=∠AEC=60°,但∠ADC≠∠AEB,根据以上推出的结论即可得出答案.
解答:∵△ABD与△AEC都是等边三角形,
∴AD=AB,AE=AC,∠ADB=∠ABD=60°,∠DAB=∠EAC=60°,
∴∠DAB+∠BAC=∠EAC+∠BAC,
∴∠DAC=∠BAE,
在△DAC和△BAE中

,
∴△DAC≌△BAE(SAS),
∴BE=DC,∠ADC=∠ABE,
∵∠BOD=180°-∠ODB-∠DBA-∠ABE
=180°-∠ODB-60°-∠ADC
=120°-(∠ODB+∠ADC)
=120°-60°=60°,
∴∠BOD=60°,∴①正确;②正确;
∵△ABD与△AEC都是等边三角形,
∴∠ADB=∠AEC=60°,但根据已知不能推出∠ADC=∠AEB,
∴说∠BDO=∠CEO错误,∴③错误;
故答案为:①②.
点评:本题考查了对等边三角形的性质,三角形的内角和定理,全等三角形的性质和判定的应用.

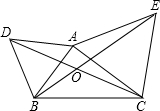
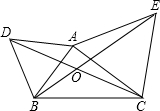 如图,△ABD与△AEC都是等边三角形,AB≠AC.下列结论中,正确的是________.
如图,△ABD与△AEC都是等边三角形,AB≠AC.下列结论中,正确的是________. ,
,


 名校课堂系列答案
名校课堂系列答案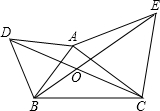 (2013•槐荫区二模)如图,△ABD与△AEC都是等边三角形,AB≠AC.下列结论中,正确的是
(2013•槐荫区二模)如图,△ABD与△AEC都是等边三角形,AB≠AC.下列结论中,正确的是