
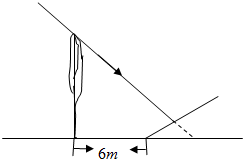
 在坡度为
在坡度为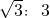 的斜坡前6米处有一高度为10米的树,当太阳照射的倾斜角为45°时,求斜坡上的树影长.
的斜坡前6米处有一高度为10米的树,当太阳照射的倾斜角为45°时,求斜坡上的树影长. 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 如图,已知斜坡AB长60米,坡角(即∠BAC)为30°,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示)修建一个平行于水平线CA的平台DE和一条新的斜坡BE.(下面两小题的结果都精确到0.1米,参考数据:
如图,已知斜坡AB长60米,坡角(即∠BAC)为30°,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示)修建一个平行于水平线CA的平台DE和一条新的斜坡BE.(下面两小题的结果都精确到0.1米,参考数据:| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知斜坡AB长60米,坡角(即∠BAC)为30°,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示)修建一个平行于水平线CA的平台DE和一条新的斜坡BE.(下面![]() 两小题的结果都精确到0.1米,参考数据:
两小题的结果都精确到0.1米,参考数据:![]() ≈1.732)
≈1.732)
(1)若修建的斜坡BE的坡度为1:0.8,则平台DE的长为 ![]() 米;
米;
(![]() 2)斜坡前的池塘内有一座建筑物GH,小明在平台E处测得建筑物顶部H的仰角(即∠HEM)为30°,测得建筑物顶部H在池塘中倒影H′的俯角为45º(即∠H′EM),测得点B、C、A、G、H、H′在同一个平面内,点C、A、G在同一条直线上,且HG⊥CG,求建筑物GH的高和AG的长。
2)斜坡前的池塘内有一座建筑物GH,小明在平台E处测得建筑物顶部H的仰角(即∠HEM)为30°,测得建筑物顶部H在池塘中倒影H′的俯角为45º(即∠H′EM),测得点B、C、A、G、H、H′在同一个平面内,点C、A、G在同一条直线上,且HG⊥CG,求建筑物GH的高和AG的长。
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com