
如图,四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点.
(1)判断四边形EFGH是何种特殊的四边形,并说明你的理由;
(2)要使四边形EFGH是菱形,四边形ABCD还应满足的一个条件是 AD=BC .
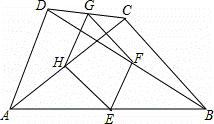
解:(1)四边形EFGH是平行四边形;
证明:在△ACD中∵G、H分别是CD、AC的中点,
∴GH∥AD,GH= AD,
在△ABC中∵E、F分别是AB、BD的中点,
∴EF∥AD,EF= AD,
∴EF∥GH,EF=GH,
∴四边形EFGH是平行四边形.
(2)要使四边形EFGH是菱形,四边形ABCD还应满足的一个条件是AD=BC.
理由如下:∵E,F分别是AB,BD的中点,
∴EF∥AD且EF= AD,
同理可得:GH∥AD且GH= AD,EH∥BC且EH= BC,
∴EF∥GH且EF=GH,
∴四边形EFGH是平行四边形,
∵AD=BC,
∴ AD= BC,
即EF=EH,
∴▱EFGH是菱形.


科目:初中数学 来源: 题型:
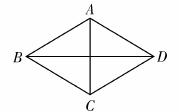
如图,四边形ABCD的对角线AC、BD互相垂直,则下列条件能判定四边 形ABCD为菱形的是( ).
形ABCD为菱形的是( ).
A.BA=BC B.AC、BD互相平分
C.AC=BD D.AB∥CD
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,已知点P0的坐标为(1,0),将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此下去,得到线段OP3,OP4,…OPn(n为正整数).那么点P6的坐标是 ,点P2014的坐标是 .
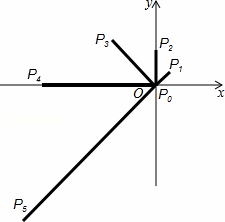
查看答案和解析>>
科目:初中数学 来源: 题型:
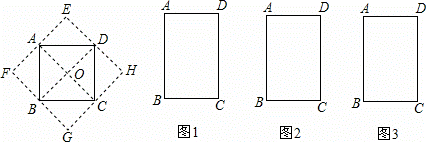
如图,正方形ABCD的两条对角线把正方形分割成四个等腰直角三角形,将这四个三角形分别沿正方形ABCD的边向外翻折,可得到一个新正方形EFGH.请你在矩形ABCD中画出分割线,将矩形分割成四个三角形,然后分别将这四个三角形沿矩形的边向外翻折,使得图1得到菱形,图2得到矩形,图3得到一般的平行四边形(只在矩形ABCD中画出分割线,说明分割线的作法,不画出翻折后的图形).
查看答案和解析>>
科目:初中数学 来源: 题型:
下列函数中:(1)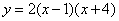 ; (2)
; (2) 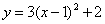 ;(3)
;(3)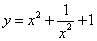 ; (4)
; (4)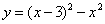 .不是二次函数的是( )
.不是二次函数的是( )
A. (1)(2) B. (3)(4) C. (1)(3) D. (2)(4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com