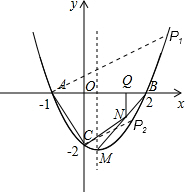
解:(1)设抛物线解析式为y=a(x+1)(x-2),
将x=0,y=-2代入得:a=1,
∴抛物线y=x
2-x-2=(x-

)
2-

,
∴顶点M的坐标为(

,-

);
(2)抛物线与y=x
2-x-2与x轴的两交点为A(-1,0),B(2,0),
设线段BM所在直线的解析式为y=kx+b,
则
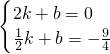
,
解得

;
故线段BM所在直线的解析式为y=

x-3,
设点N的坐标为(x,-t),
∵点N在线段BM上,
∴-t=

x-3,
∴x=-

t+2,
∴S
四边形NQAC=S
△AOC+S
梯形OQNC=

×1×2+

×(2+t)×(-

t+2)=-

t
2+

t+3,
∴S与t之间的函数关系式为S=-

t
2+

t+3,自变量t的取值范围为0<t<

;
(3)假设存在符合条件的点P,设点P的坐标为P(m,n),则m>

且n=m
2-m-2;
PA
2=(m+1)
2+n
2,PC
2=m
2+(n+2)
2,AC
2=5,
分以下几种情况讨论:
①若∠PAC=90°,则PC
2=PA
2+AC
2.
∴
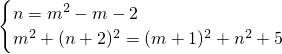
,
解得:m
1=

,m
2=-1;
∵m>

,∴m=

,
∴P
1(

,

);
②若∠PCA=90°,则PA
2=PC
2+AC
2,
则
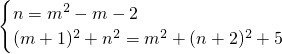
,
解得:m
3=

,m
4=0,
∵m>

,
∴m=

,
∴P
2(

,-

),
当点P在对称轴右侧时,PA>AC,
∴边AC的对角∠APC不可能是直角,
∴存在符合条件的点P,坐标分别为P
1(

,

);P
2(

,-

).
分析:(1)根据A与B的横坐标,设出抛物线的二根式方程,将C坐标代入求出a的值,确定出抛物线解析式,将解析式化为顶点坐标式,即可求出抛物线顶点M的坐标.
(2)根据抛物线的解析式可求出A、B、C三点的坐标,进而可求出直线BM的解析式,已知了QN=t,即N点纵坐标为-t,代入直线BM的解析式中,可求得Q点的横坐标即OQ得长,分别求出△OAC、梯形QNCO的面积,它们的面积和即为所求的四边形QNCO的面积,由此可求出S、t的函数关系式.
(3)根据函数的图象及A、C的位置,可明显的看出∠APC不可能是直角,因此此题要分两种情况讨论:
①∠PAC=90°,设出点P的坐标,然后表示出AC
2、PA
2、PC
2的值,根据勾股定理可得到关于P点横、纵坐标的等量关系式,联立抛物线的解析式,即可求出此时点P的坐标;
②∠PCA=90°,解法同①.
点评:此题考查了二次函数综合题,涉及的知识有:坐标与图形性质,待定系数法求二次函数解析式,二次函数的图象与性质,利用了分类讨论的思想,熟练掌握待定系数法是解本题的关键.

 已知二次函数的图象如图所示,
已知二次函数的图象如图所示, 解:(1)设抛物线解析式为y=a(x+1)(x-2),
解:(1)设抛物线解析式为y=a(x+1)(x-2), )2-
)2- ,
, ,-
,- );
);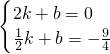 ,
, ;
; x-3,
x-3, x-3,
x-3, t+2,
t+2, ×1×2+
×1×2+ ×(2+t)×(-
×(2+t)×(- t+2)=-
t+2)=- t2+
t2+ t+3,
t+3, t2+
t2+ t+3,自变量t的取值范围为0<t<
t+3,自变量t的取值范围为0<t< ;
; 且n=m2-m-2;
且n=m2-m-2;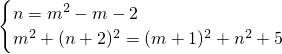 ,
, ,m2=-1;
,m2=-1; ,∴m=
,∴m= ,
, ,
, );
);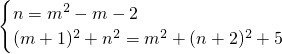 ,
, ,m4=0,
,m4=0, ,
, ,
, ,-
,- ),
), ,
, );P2(
);P2( ,-
,- ).
).

 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案 已知二次函数的图象如右图,则下列结论中,正确的结论有( )
已知二次函数的图象如右图,则下列结论中,正确的结论有( ) 已知二次函数的图象如图所示,
已知二次函数的图象如图所示,