Question

4．如图，点B、C分别在函数$y=\frac{6}{x}$的图象上，AB∥x轴，AC∥y轴，已知点A的坐标为（2，m）（0＜m＜3），延长OA反比例函数$y=\frac{6}{x}$的图象交于点P

（1）当点P横坐标为3，求m的值；
（2）连接CO，当AC=OA时，求m的值；
（3）连接BP、CP，$\frac{{{S_{△ABP}}}}{{{S_{△ACP}}}}$的值是否随m的变化而变化？若变化，说明理由；若不变，求出$\frac{{{S_{△ABP}}}}{{{S_{△ACP}}}}$的值．

Answer 1

分析 （1）延长CA交x轴于点E，过点P作PF⊥x轴于点F，由点P的横坐标为3即可求出点P的坐标，再由CE∥PF即可得出比例关系$\frac{PF}{AE}=\frac{OF}{OE}$，代入数据即可求出m值；
（2）由点A的坐标可求出点C的坐标，由此可得出AC的长度，利用两点间的距离公式即可求出OA的长度，再由AC=OA即可得出关于m的方程，解方程即可得出m值；
（3）设直线OP的解析式为y=kx，由点A的坐标利用待定系数法即可求出直线OP的解析式，再根据三角形的面积公式找出S_△ABP和S_△ACP，由此即可得出结论．

解答 解：（1）延长CA交x轴于点E，过点P作PF⊥x轴于点F，则CE∥PF，如图1所示．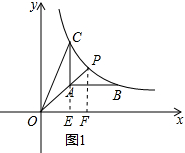
∵点P在反比例函数$y=\frac{6}{x}$的图象上，且点P的横坐标为3，
∴点P的坐标为（3，2），
∵CE∥PF，
∴$\frac{PF}{AE}=\frac{OF}{OE}$，即$\frac{2}{m}$=$\frac{3}{2}$，
解得：m=$\frac{4}{3}$．
（2）令$y=\frac{6}{x}$中x=2，则y=3，
∴点C（2，3），
∴AC=3-m，OA²=4+m²，
∵AC=OA，
∴（3-m）²=4+m²，
解得：m=$\frac{5}{6}$．
（3）设直线OP的解析式为y=kx，
将点A（2，m）代入到y=kx中，
得：m=2k，解得：k=$\frac{m}{2}$，
∴直线OP的解析式为y=$\frac{m}{2}$x．
联立直线OP与反比例函数解析式得：$\left\{\begin{array}{l}{y=\frac{m}{2}x}\\{y=\frac{6}{x}}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{x=\frac{2\sqrt{3m}}{m}}\\{y=\sqrt{3m}}\end{array}\right.$，或$\left\{\begin{array}{l}{x=-\frac{2\sqrt{3m}}{m}}\\{y=-\sqrt{3m}}\end{array}\right.$（舍去），
∴点P（$\frac{2\sqrt{3m}}{m}$，$\sqrt{3m}$）．
令y=$\frac{6}{x}$中y=m，则x=$\frac{6}{m}$，
∴点B（$\frac{6}{m}$，m），点C（2，3），
∴S_△ABP=$\frac{1}{2}$AB•（y_P-y_A）=$\frac{1}{2}$•（$\frac{6}{m}$-2）•（$\sqrt{3m}$-m），S_△ACP=$\frac{1}{2}$AC•（x_P-x_A）=$\frac{1}{2}$•（3-m）•（$\frac{2\sqrt{3m}}{m}$-2），
∴$\frac{{S}_{△ABP}}{{S}_{ACP}}$=$\frac{\frac{1}{2}•（\frac{6}{m}-2）•（\sqrt{3m}-m）}{\frac{1}{2}•（3-m）•（\frac{2\sqrt{3m}}{m}-2）}$=1．
故连接BP、CP，$\frac{{S}_{△ABP}}{{S}_{ACP}}$的值为定值1．

点评 本题考查了反比例函数图象上点的坐标特征、待定系数法求函数解析式以及三角形的面积公式，解题的关键是：（1）根据比例关系$\frac{PF}{AE}=\frac{OF}{OE}$找出关于m的方程；（2）根据AC=OA找出关于m的方程；（3）用含m的代数式表示出S_△ABP和S_△ACP．本题属于中档题，难度不大，解决该题型题目时，通过联立直线与反比例函数解析式成方程组，解方程组找出交点坐标是关键．