练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．解方程与计算
    （1）利用平方根解方程：2（x-1）2-6=0
    （2）计算：$\sqrt{（-10）^{2}}$•$\sqrt{\frac{1}{100}}$-$\sqrt{25}$+（$\sqrt{2}$）2．

    分析 （1）方程整理后，利用平方根定义开方即可求出解；
    （2）原式利用二次根式性质，以及平方根定义计算即可得到结果．

    解答 解：（1）方程整理得：（x-1）2=3，
    开方得：x-1=±$\sqrt{3}$，
    解得：x1=1+$\sqrt{3}$，x2=1-$\sqrt{3}$；
    （2）原式=10×$\frac{1}{10}$-5+2=1-5+2=-2．

    点评 此题考查了实数的运算，以及平方根，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    11．如图，?AOBC中，对角线交于点E，双曲线经过A、E两点，若?AOBC的面积为12，则k=4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．我们把两条中线互相垂直的三角形称为“中垂三角形”．例如图1，图2，图3中，AF，BE是△ABC的中线，AF⊥BE，垂足为P．像△ABC这样的三角形均为“中垂三角形”．设BC=a，AC=b，AB=c．
    特例探索
    （1）①如图1，当∠ABE=45°，$c=2\sqrt{2}$时，a=2$\sqrt{5}$，b=2$\sqrt{5}$；
    ②如图2，当∠ABE=30°，c=4时，求a和b的值
    归纳证明
    （2）请你观察（1）中的计算结果，猜想三者之间的关系，用等式表示出来，并利用图3证明你发现的关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

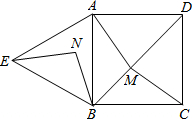    9．如图，△ABE是等边三角形，M是正方形ABCD对角线BD（不含B点）上任意一点，BM=BN，∠ABN=15°（点N在AB的左侧），当AM+BM+CM的最小值为$\sqrt{3}$+1时，正方形的边长为$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．分式$\frac{x}{x^3}、\frac{3a+1}{3a+b}、\frac{m+n}{{{m^2}-{n^2}}}、\frac{2-2x}{2x}$中，最简分式的个数是1个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．用科学记数法表示：0.00002016=2.016×10-5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

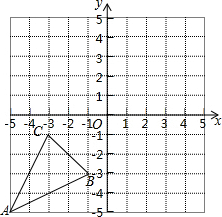    13．如图，在平面直角坐标系中，△ABC的顶点坐标是A（-5，5），B（-1，-3），C（-3．-1）
    按要求画出变换后的图形：
    （1）画出△ABC关于y轴对称的△A1B1C1；
    （2）以原点O为旋转中心，把△A1B1C1逆时针旋转90°，得到△A2B2C2
    ；
    （3）△ABC和△A2B2C2组成的图形是轴对称图形吗？如果是，请直接写出对称轴所在的直线的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．计算（2$-\sqrt{3}）$2013×$（2+\sqrt{3}）^{2014}$$+（π-\sqrt{3}）^{0}$+|$\sqrt{3}$-2|+9×3-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．如图，点O，A在数轴上表示的数分别是0，0.1．将线段OA分成100等份，其分点由左向右依次为M1，M2，…，M99；再将线段OM1，分成100等份，其分点由左向右依次为N1，N2，…，N99；继续将线段ON1分成100等份，其分点由左向右依次为P1，P2．…，P99．则点P26所表示的数用科学记数法表示为2.6×10-6．

    查看答案和解析>>

    同步练习册答案