练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，四边形ABCD的对角线交于点O，下列哪组条件不能判断四边形ABCD是平行四边形（　　）

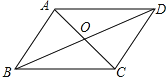
    A. ， B. ，

    C. ， D. ，

    【答案】B

    【解析】

    根据平行四边形的判定方法，对每个选项进行筛选可得答案．

    A、∵OA=OC，OB=OD，

    ∴四边形ABCD是平行四边形，故A选项不符合题意；

    B、AB=CD，AO=CO不能证明四边形ABCD是平行四边形，故本选项符合题意；

    C、∵AD//BC，AD=BC，

    ∴四边形ABCD是平行四边形，故C选项不符合题意；

    D、∵AB∥CD，

    ∴∠ABC+∠BCD=180°，∠BAD+∠ADC=180°，

    又∵∠BAD=∠BCD，

    ∴∠ABC=∠ADC，

    ∵∠BAD=∠BCD，∠ABC=∠ADC，

    ∴四边形ABCD是平行四边形，故D选项不符合题意，

    故选B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某校随机选取了名学生，对他们喜欢的运动项目进行调查，整理成以下统计表，其中“√”表示喜欢，“×”表示不喜欢.

    项目
    学生数

    长跑

    短跑

    跳绳

    跳远

    200

    √

    ×

    √

    √

    300

    ×

    √

    ×

    √

    150

    √

    √

    √

    ×

    200

    √

    ×

    √

    ×

    150

    √

    ×

    ×

    ×

    (1)估计该校学生同时喜欢短跑和跳绳的概率；

    (2)估计该校学生在长跑、短跑、跳绳、跳远中同时喜欢三个项目的概率；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

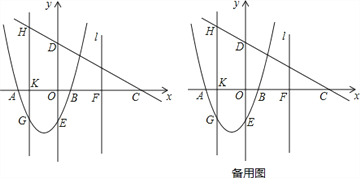
    【题目】如图，抛物线y=ax2+bx-3交x轴于点A（﹣3，0），点B（1，0），交y轴于点E．点C是点A关于点B的对称点，点F是线段BC的中点，直线过点F且与y轴平行．直线y=kx+3过点C，交y轴于D点．

    （1）求抛物线的函数表达式；

    （2）点K为线段AB上一动点，过点K作x轴的垂线与直线CD交于点H，与抛物线交于点G，求线段HG长度的最大值；

    （3）在直线上取点M，在抛物线上取点N，使以点A，C，M，N为顶点的四边形是平行四边形，求点N的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某楼盘一楼是车库（暂不出售），二楼至二十三楼均为商品房（对外销售）．商品房售价方案如下：第八层售价为4000元米，从第八层起每上升一层．每平方米的售价增加50元；反之，楼层每下降一层，每平方米的售价减少30元．已知商品房每套面积均为120平方米，开发商为购买者制定了两种购房方案：方案一：购买者先交纳首付金额（商品房总价的，再办理分期付款（即贷款）．方案二：购买者若一次付清所有房款，则享受的优惠，并免收五年物业管理费（已知每月物业管理费为元）．

    （1）请用含楼层（，是正整数）的代数式表示售价y（元/平方米）；

    （2）小张已筹到160000元，若用方案一购房，他可以首付哪些楼层的商品房呢？

    （3）老王想在此楼盘买房，有人建议老王使用方案二购买第十六层，但他认为此方案还不如不免收物业管理费而直接再多享受的优惠划算．你认为老王的说法一定正确吗？请用具体数据阐明你的看法．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，AB=AC，AD、AE分别是∠BAC与∠BAC的外角的平分线，BE⊥AE．求证：AB=DE.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，每个小正方形的边长为1cm

    （1）求四边形ABCD的面积；

    （2）四边形ABCD中有直角吗？若有，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】观察下列方程的特征及其解的特点．

    ①x＋＝－3的解为x1＝－1，x2＝－2；

    ②x＋＝－5的解为x1＝－2，x2＝－3；

    ③x＋＝－7的解为x1＝－3，x2＝－4.

    解答下列问题：

    (1)请你写出一个符合上述特征的方程为________，其解为________；

    (2)根据这类方程的特征，写出第n个方程为________，其解为________；

    (3)请利用(2)的结论，求关于x的方程x＋＝－2(n＋2)(其中n为正整数)的解．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小红星期天从家里出发骑车去舅舅家做客，当她骑了一段路时，想起要买个礼物送给表弟，于是又折回到刚经过的一家商店，买好礼物后又继续骑车去舅舅家，以下是她本次去舅舅家所用的时间与路程的关系式示意图．根据图中提供的信息回答下列问题：

    (1)小红家到舅舅家的路程是______米，小红在商店停留了______分钟；

    (2)在整个去舅舅家的途中哪个时间段小红骑车速度最快，最快的速度是多少米/分

    (3)本次去舅舅家的行程中，小红一共行驶了多少米？一共用了多少分钟？

    查看答案和解析>>

    同步练习册答案