
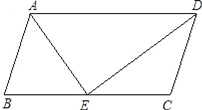
【题目】如图,已知平行四边形ABCD,DE是∠ADC的角平分线,交BC于点E.
(1)求证:CD=CE;
(2)若BE=CE,∠B=80°,求∠DAE的度数.
【答案】(1)证明见解析;(2)∠DAE=50°.
【解析】试题分析:(1)根据DE是∠ADC的角平分线得到∠1=∠2,再根据平行四边形的性质得到∠1=∠3,所以∠2=∠3,根据等角对等边即可得证;
(2)先根据BE=CE结合CD=CE得到△ABE是等腰三角形,求出∠BAE的度数,再根据平行四边形邻角互补得到∠BAD=100°,所以∠DAE可求.
(1)证明:如图,在平行四边形ABCD中,
∵AD∥BC
∴∠1=∠3
又∵∠1=∠2,
∴∠2=∠3,
∴CD=CE;
(2)解:∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,
又∵CD=CE,BE=CE,
∴AB=BE,
∴∠BAE=∠BEA.
∵∠B=80°,
∴∠BAE=50°,
∴∠DAE=180°﹣50°﹣80°=50°.
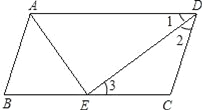
点睛:本题主要考查平行四边形的性质,根据平行四边形的性质中对边平行,以及DE是∠ADC的平分线,证明△DEC是等腰三角形,以类似的方法也可以求出∠DAE的角度.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】“城市发展 交通先行”,成都市今年在中心城区启动了缓堵保畅的二环路高架桥快速通道建设工程,建成后将大大提升二环路的通行能力.研究表明,某种情况下,高架桥上的车流速度V(单位:千米/时)是车流密度x(单位:辆/千米)的函数,且当0<x≤28时,V=80;当28<x≤188时,V是x的一次函数.函数关系如图所示. 
(1)求当28<x≤188时,V关于x的函数表达式;
(2)若车流速度V不低于50千米/时,求当车流密度x为多少时,车流量P(单位:辆/时)达到最大,并求出这一最大值. (注:车流量是单位时间内通过观测点的车辆数,计算公式为:车流量=车流速度×车流密度)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校某年级秋游,若租用48座客车若干辆,则正好坐满;若租用64座客车,则能少租1辆,且有一辆车没有坐满,但超过一半.
(1)需租用48座客车多少辆? 解:设需租用48座客车x辆.则需租用64座客车辆.当租用64座客车时,未坐满的那辆车还有个空位(用含x的代数式表示).由题意,可得不等式组:解这个不等式组,得: .
因此,需租用48座客车辆.
(2)若租用48座客车每辆250元,租用64座客车每辆300元,应租用哪种客车较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C、D、E、F是⊙O的六等分点. 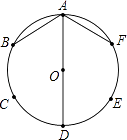
(1)连接AB、AD、AF,求证:AB+AF=AD;
(2)若P是圆周上异于已知六等分点的动点,连接PB、PD、PF,写出这三条线段长度的数量关系(不必说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一带一路”涉及沿线65个国家,总涉及人口约44000……,用科学记数法表示为4.4×109,则原数中“0”的个数为( )
A.6B.7C.8D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
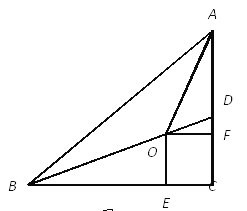
【题目】如图,在Rt△ABC中,∠C=90,BD是△ABC的角平分线,点O在BD上,分别过点O作OE⊥BC,OF⊥AC,垂足为E,F,且OE=OF.
(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com