练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11．如图，在半径为5cm的⊙O中，弦AB=6cm，OC⊥AB于点C，则OC=（　　）
    A．3cmB．4cmC．5cmD．6cm

    分析 连接OA，先利用垂径定理得出AC的长，再由勾股定理得出OC的长即可解答．

    解答 解：连接OA，
    ∵AB=6cm，OC⊥AB于点C，
    ∴AC=$\frac{1}{2}$AB=$\frac{1}{2}$×6=3cm，
    ∵⊙O的半径为5cm，
    ∴OC=$\sqrt{O{A}^{2}-A{C}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4cm，
    故选B．

    点评 本题考查了垂径定理，以及勾股定理，熟练掌握垂径定理的应用是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    1．在Rt△ABC中，∠ABC=90°，BD平分∠ABC，点D在△ABC外，∠ADC=135°，且∠ADB=∠CDE，求证：AE=CE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

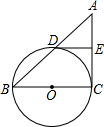    2．如图，已知BC是⊙O的直径，AC切⊙O于点C，AB交⊙O于点D，E为AC的中点，连结DE．
    （1）若AD=DB，OC=5，求切线AC的长；
    （2）求证：ED是⊙O的切线．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．如图，AB∥CD，点E，F分别在AB，CD上，连接EF，∠AEF、∠CFE的平分线交于点G，∠BEF、∠DFE的平分线交于点H．
    （1）求证：四边形EGFH是矩形；
    （2）小明在完成（1）的证明后继续进行了探索，过G作MN∥EF，分别交AB，CD于点M，N，过H作PQ∥EF，分别交AB，CD于点P，Q，得到四边形MNQP，此时，他猜想四边形MNQP是菱形，请在下列框中补全他的证明思路．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．下列运算正确的是（　　）
    A．a•a3=a3B．2（a-b）=2a-bC．（a3）2=a5D．a2-2a2=-a2

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．某射击运动员在一次射击训练中，共射击了6次，所得成绩（单位：环）为：6、8、7、7、8、9，这组数据的中位数是7.5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．交通指数是交通拥堵指数的简称，是综合反映道路畅通或拥堵的概念．其指数在100以内为畅通，200以上为严重拥堵，从某市交通指挥中心选取了5月1日至14日的交通状况，依据交通指数数据绘制的折线统计图如图所示，某人随机选取了5月1日至14日的某一天到达该市．
    （1）请结合折线图分别找出交通为畅通和严重拥堵的天数；
    （2）求此人到达当天的交通为严重拥堵的概率；
    （3）由图判断从哪天开始连续三天的交通指数方差最大？（直接判断，不要求计算）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

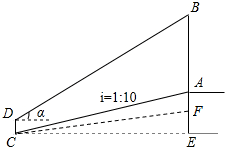    20．数学活动课上，老师和学生一起去测量学校升旗台上旗杆AB的高度．如图，老师测得升旗台前斜坡FC的坡比为iFC=1：10（即EF：CE=1：10），学生小明站在离升旗台水平距离为35m（即CE=35m）处的C点，测得旗杆顶端B的仰角为α．已知tanα=$\frac{3}{7}$，升旗台高AF=1m，小明身高CD=1.6m，请帮小明计算出旗杆AB的高度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．某地一天的最高气温是12℃，最低气温是2℃，则该地这天的温差是（　　）
    A．-10℃B．10℃C．14℃D．-14℃

    查看答案和解析>>

    同步练习册答案