
【题目】如图,在△ABC中,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB. 
(1)求证:直线BF是⊙O的切线;
(2)若点D,点E分别是弧AB的三等分点,当AD=5时,求BF的长;
(3)在(2)的条件下,如果以点C为圆心,r为半径的圆上总存在不同的两点到点O的距离为5,求r的取值范围.
【答案】
(1)证明:如图,∵∠CBF=∠CFB,
∴CB=CF.
又∵AC=CF,
∴CB= ![]() AF,
AF,
∴△ABF是直角三角形,
∴∠ABF=90°,即AB⊥BF.
又∵AB是直径,
∴直线BF是⊙O的切线
(2)解:如图,连接DO,EO,
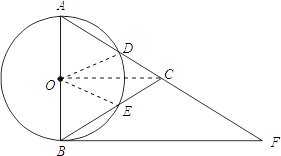
∵点D,点E分别是弧AB的三等分点,
∴∠AOD=60°.
又∵OA=OD,
∴△AOD是等边三角形,
∴OA=AD=OD=5,∠OAD=60°,
∴AB=10.
∴在Rt△ABF中,∠ABF=90°,BF=ABtan60°=10 ![]() ,即BF=10
,即BF=10 ![]()
(3)如图,连接OC.则OC是Rt△ABF的中位线,

∵由(2)知,BF=10 ![]() ,
,
∴圆心距OC= ![]() ,
,
∵⊙O半径OA=5.
∴ ![]() <r<
<r< ![]() .
.
【解析】(1)欲证明直线BF是⊙O的切线,只需证明AB⊥BF;(2)根据圆心角、弧、弦间的关系,等边三角形的判定证得△AOD是等边三角形,所以在Rt△ABF中,∠ABF=90°,∠OAD=60°,AB=10,则利用∠A的正切三角函数的定义来求BF边的长度;(3)根据已知条件知⊙O与⊙C相交.


 作业辅导系列答案
作业辅导系列答案科目:初中数学 来源: 题型:
【题目】如图,小山岗的斜坡AC的坡角α=45°,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,小山岗的高AB约为(结果取整数,参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50)( )
A.164m
B.178m
C.200m
D.1618m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB′C′D′,边BC与D′C′交于点O,则四边形ABOD′的周长是( )
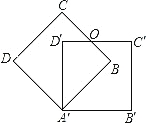
A. 6![]() B. 6C. 3
B. 6C. 3![]() D. 3+3
D. 3+3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一矩形纸片OABC放在平面直角坐标系中,O为原点,点A在x轴上,点C在y轴上,OA=10,OC=8,如图在OC边上取一点D,将△BCD沿BD折叠,使点C恰好落在OA边上,记作E点;
(1)求点E的坐标及折痕DB的长;
(2)在x轴上取两点M、N(点M在点N的左侧),且MN=4.5,求使四边形BDMN的周长最短的点M、点N的坐标。
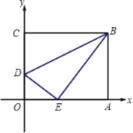
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲厂有某种原料198吨,每天用去12吨,乙厂有同样的原料121吨,每天运进7吨,问多少天后甲厂原料是乙厂原料的![]() ,设x天后甲厂原料是乙厂原料的
,设x天后甲厂原料是乙厂原料的![]() ,则下列正确的方程是( )
,则下列正确的方程是( )
A. 198-12x=![]() (121-7x) B.
(121-7x) B. ![]() (198-12x)= 121-7x
(198-12x)= 121-7x
C. ![]() (198-12x)= 121+7x D. 198-12x=
(198-12x)= 121+7x D. 198-12x= ![]() (121+7x)
(121+7x)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校学生对A《最强大脑》、B《朗读者》、C《中国诗词大会》、D《出彩中国人》四个电视节目的喜爱情况,随机抽取了m学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),将调查结果绘制成如下两幅不完整的统计图(如图1和图2):
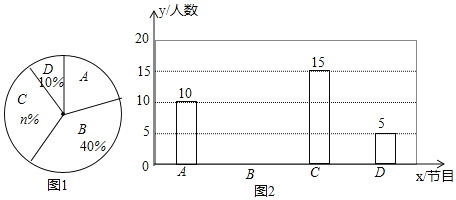
根据统计图提供的信息,回答下列问题;
(1)m= ,n= ;
(2)扇形统计图中,喜爱《最强大脑》节目所对应的扇形的圆心角度数是 度.
(3)根据以上信息直接在答题卡中补全条形统计图;
(4)根据抽样调查结果,请你估计该校6000名学生中有多少学生最喜欢《中国诗词大会》节目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程![]() ﹣1的步骤如下:
﹣1的步骤如下:
(解析)第一步:![]() ﹣1(分数的基本性质)
﹣1(分数的基本性质)
第二步:2x﹣1=3(2x+8)﹣3……(①)
第三步:2x﹣1=6x+24﹣3……(②)
第四步:2x﹣6x=24﹣3+1……(③)
第五步:﹣4x=22(④)
第六步:x=﹣![]() ……(⑤)
……(⑤)
以上解方程第二步到第六步的计算依据有:①去括号法则.②等式性质一.③等式性质二.④合并同类项法则.请选择排序完全正确的一个选项( )
A. ②①③④② B. ②①③④③ C. ③①②④③ D. ③①④②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知A(-1,5),B(4,2),C(-1,0)三点.
(1)点A的对称点A′的坐标为(1,-5),点B关于x轴的对称点B′的坐标为________,点C关于y轴的对称点C′的坐标为________;
(2)求(1)中的△A′B′C′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某船在A、B两地之间航行,顺水航行需要4小时,逆水行需要5小时,水流速度为2千米/时.
(1)求船在静水中的速度.
(2)若船从A地顺水航行到B地,然后逆流返回,到达距离A地26千米的C地,一共航行了多少小时?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com