
【题目】如图,菱形ABCD的周长为16,若 ![]() ,E是AB的中点,则点E的坐标为 .
,E是AB的中点,则点E的坐标为 . 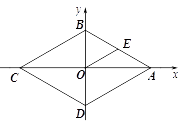
【答案】![]()
【解析】解:如图所示,过E作EM⊥AC,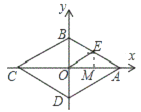
已知四边形ABCD是菱形,且周长为16,∠BAD=60°,根据菱形的性质可得AB=CD-BC=AD=4,AC⊥DB,∠BAO= ![]() ∠BAD=30°,又因E是AB的中点,根据直角三角形中,斜边的中线等于斜边的一半可得EO=EA=EB=
∠BAD=30°,又因E是AB的中点,根据直角三角形中,斜边的中线等于斜边的一半可得EO=EA=EB= ![]() AB=2,根据等腰三角形的性质可得∠BAO=∠EOA=30°,由直角三角形中,30°的锐角所对的直角边等于斜边的一半可得EM=
AB=2,根据等腰三角形的性质可得∠BAO=∠EOA=30°,由直角三角形中,30°的锐角所对的直角边等于斜边的一半可得EM= ![]() OE=1,在Rt△OME中,由勾股定理可得OM=
OE=1,在Rt△OME中,由勾股定理可得OM= ![]() ,所以点E的坐标为(
,所以点E的坐标为( ![]() ,1),
,1),
故选 ![]() .
.
【考点精析】掌握勾股定理的概念和菱形的性质是解答本题的根本,需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图1,将正方形 ![]() 置于平面直角坐标系中,其中
置于平面直角坐标系中,其中 ![]() 边在
边在 ![]() 轴上,其余各边均与坐标轴平行.直线
轴上,其余各边均与坐标轴平行.直线 ![]() 沿
沿 ![]() 轴的负方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形
轴的负方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形 ![]() 的边所截得的线段长为
的边所截得的线段长为 ![]() ,平移的时间为
,平移的时间为 ![]() (秒),
(秒), ![]() 与
与 ![]() 的函数图象如图2所示,则图1中的点
的函数图象如图2所示,则图1中的点 ![]() 的坐标为 , 图2中
的坐标为 , 图2中 ![]() 的值为.
的值为.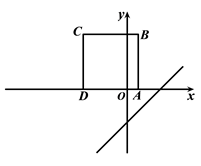

图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形 ![]() 中,
中, ![]() ,
, ![]() ,点
,点 ![]() 是
是 ![]() 边上一点,过点
边上一点,过点 ![]() 作
作 ![]() ,交射线
,交射线 ![]() 于点
于点 ![]() ,交射线
,交射线 ![]() 于点
于点 ![]() .
.
(1)如图1,若 ![]() ,则
,则 ![]() 度;
度;
(2)当以 ![]() ,
, ![]() ,
, ![]() 为顶点的三角形是等边三角形时,依题意在图2中补全图形并求
为顶点的三角形是等边三角形时,依题意在图2中补全图形并求 ![]() 的长;
的长;
(3)过点 ![]() 作
作 ![]() ∥
∥ ![]() 交射线
交射线 ![]() 于点
于点 ![]() ,请探究:当
,请探究:当 ![]() 为何值时,以
为何值时,以 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为顶点的四边形是平行四边形.
为顶点的四边形是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(﹣8,0),点P的坐标为(-![]() ,0),直线y=
,0),直线y=![]() x+b过点A,交y轴于点B,以点P为圆心,以PA为半径的圆交x轴于点C.
x+b过点A,交y轴于点B,以点P为圆心,以PA为半径的圆交x轴于点C.
(1)判断点B是否在⊙P上?说明理由.
(2)求过A、B、C三点的抛物线的解析式;并求抛物线与⊙P另外一个交点为D的坐标.
(3)⊙P上是否存在一点Q,使以A、P、B、Q为顶点的四边形是菱形?若存在,求出点Q的坐标;若不存在,请说明理由.
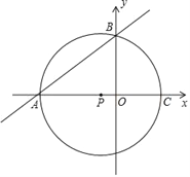
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
(1)如图①,∠AOB=60°,OD平分∠BOC,OE平分∠AOC,则∠EOD=度;
(2)若∠AOB=90°,其它条件不变,则∠EOD=;
(3)若∠AOB=α,其它条件不变,则∠EOD= .
(4)类比应用:如图②,已知线段AB,C是线段AB上任一点,D、E分别是AC、CB的中点,试猜想DE与AB的数量关系为 , 并写出求解过程.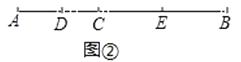
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,为了山更绿、水更清,某区大力实施生态修复工程,发展林业产业,确保到2021年实现全区森林覆盖率达到72.6%的目标.已知该区2019年全区森林覆盖率为60%,设从2019年起该区森林覆盖率年平均增长率为x,则x=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b、c是△ABC的三边长,且方程a(1+x2)+2bx﹣c(1﹣x2)=0的两根相等,则△ABC为( )
A. 等腰三角形 B. 直角三角形 C. 等边三角形 D. 任意三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCO中,O为坐标原点,A在y轴上,C在x轴上,B的坐标为(8,6),P是线段BC上动点,点D是直线y=2x﹣6上第一象限的点,若△APD是等腰直角三角形,则点D的坐标为_____________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com