
【题目】在矩形 ![]() 中,
中, ![]() ,
, ![]() ,点
,点 ![]() 是
是 ![]() 边上一点,过点
边上一点,过点 ![]() 作
作 ![]() ,交射线
,交射线 ![]() 于点
于点 ![]() ,交射线
,交射线 ![]() 于点
于点 ![]() .
.
(1)如图1,若 ![]() ,则
,则 ![]() 度;
度;
(2)当以 ![]() ,
, ![]() ,
, ![]() 为顶点的三角形是等边三角形时,依题意在图2中补全图形并求
为顶点的三角形是等边三角形时,依题意在图2中补全图形并求 ![]() 的长;
的长;
(3)过点 ![]() 作
作 ![]() ∥
∥ ![]() 交射线
交射线 ![]() 于点
于点 ![]() ,请探究:当
,请探究:当 ![]() 为何值时,以
为何值时,以 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为顶点的四边形是平行四边形.
为顶点的四边形是平行四边形.
【答案】
(1)90
(2)
解:补全图形,如图所示.
∵四边形ABCD是矩形,
∴BC=AD=12,∠D=90°.
∵△ ![]() 是等边三角形,
是等边三角形,
∴GC=FC , ![]() .
.
∵∠2=∠3,
∴∠3=60°
在Rt△CDF中,DC=8 ,
∴ ![]() .
.
∴ ![]() .
.
∴ ![]() .
.
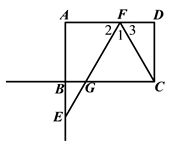
(3)
解:解法一:
过点F作FK⊥BC于点K,如图.
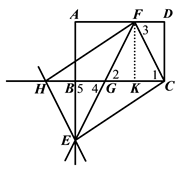
∵四边形ABCD是矩形,
∴∠5=∠ABC=90°,AD//BC.
∴∠1=∠3,∠2=∠AFG.
∵∠3=∠AFG,
∴∠1=∠2.
∴FG=FC.
∴GK=CK.
∵四边形FHEC是平行四边形,
∴FG=EG.
∵∠2=∠4,∠FKG=∠5=90°,
∴△FGK≌△EGB.
∴ ![]() .
.
∴当 ![]() 时,以
时,以 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为顶点的四边形是平行四边形.
为顶点的四边形是平行四边形.
解法二:如图.
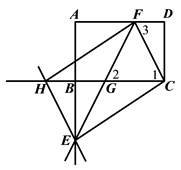
∵四边形ABCD是矩形,
∴∠ABG=90°,AD//BC.
∴∠1=∠3,∠2=∠AFG.
∵∠3=∠AFG,
∴∠1=∠2.
∴FG=FC.
∵四边形FHEC是平行四边形,
∴CG = HG ,FG=EG,HE=FC.
∴EG=EH.
又∵∠ABG=90°,
∴BG=BH=x.
∴CG=HG=2x.
∴x+2x=12.
∴x=4.
∴当 ![]() 时,以
时,以 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为顶点的四边形是平行四边形
为顶点的四边形是平行四边形
【解析】 (1)由矩形的性质得AD∥BC,∠D=90°,所以∠AFE=∠FGB,∠DFC=∠FCG,进而求得∠FGC=∠FCG,得到FC的长,再利用三角函数求得∠DFC=45°,即可得 ∠CFG=90°;
(2)先画出图形,由矩形与等边三角形的性质得到∠DFC=60°,利用三角函数求得FC的长,即为GC的长,再求BG即可;
(3)过点F作FK⊥BC于点K,由矩形的性质推出∠KCF=∠KGF,FG=FC,所以GK=CK.因为四边形FHEC是平行四边形,所以FG=EG.可得△FGK≌△EGB.所以BG=GK=KC= ![]() =4.
=4.
【考点精析】认真审题,首先需要了解等边三角形的性质(等边三角形的三个角都相等并且每个角都是60°),还要掌握平行四边形的性质(平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】A、B两站间的路程为448千米,一列慢车从A站出发,每小时行驶60千米;一列快车从B站出发,每小时行驶80千米,问:
(1)两车同时开出,相向而行,出发后多少小时相遇?
(2)两车相向而行,慢车先开出28分钟,快车开出后多少小时两车相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步加强中小学生近视眼的防控工作,某地区教育主管部门对初二年级学生的视力进行了一次抽样调查,经数据分组整理,绘制的频数分布表与频数分布直方图的一部分如下(每组含前一个边界值,不含后一个边界值):
请根据以上信息解答下列问题:
(1)表中的 ![]() ,
, ![]() ;
;
(2)在图中补全频数分布直方图;
(3)若视力在 ![]() 以上(含
以上(含 ![]() )均属正常,根据抽样调查数据,估计该地区6200名初二年级学生视力正常的有人.
)均属正常,根据抽样调查数据,估计该地区6200名初二年级学生视力正常的有人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.
(1)求每套队服和每个足球的价格是多少?
(2)若城区四校联合购买100套队服和a个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用;
(3)假如你是本次购买任务的负责人,你认为到哪家商场购买比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的( ).
A.在同一平面内,两条直线的位置只有两种:相交和垂直.
B.有且只有一条直线垂直于已知直线.
C.如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
D.从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴,
轴, ![]() 轴分别交于点A、B,抛物线
轴分别交于点A、B,抛物线![]() 经过点A和点B,与x轴的另一个交点为C,动点D从点A出发,以每秒1个单位长度的速度向O点运动,同时动点E从点B出发,以每秒2个单位长度的速度向A点运动,设运动的时间为t秒,0﹤t﹤5.
经过点A和点B,与x轴的另一个交点为C,动点D从点A出发,以每秒1个单位长度的速度向O点运动,同时动点E从点B出发,以每秒2个单位长度的速度向A点运动,设运动的时间为t秒,0﹤t﹤5.
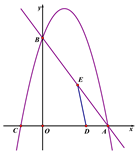
(1)求抛物线的解析式;
(2)当t为何值时,以A、D、E为顶点的三角形与△AOB相似;
(3)当△ADE为等腰三角形时,求t的值;
(4)抛物线上是否存在一点F,使得以A、B、D、F为顶点的四边形是平行四边形?若存在,直接写出F点的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.同号两数相乘,取原来的符号
B.一个数与﹣1相乘,积为该数的相反数
C.一个数与0相乘仍得这个数
D.两个数相乘,积大于任何一个乘数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com