
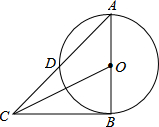
 如图,在⊙O中,AB为直径,AD为弦,过点B的切线与AD的延长线交于点C.已知∠C=40°,则∠DBA的度数是40°.
如图,在⊙O中,AB为直径,AD为弦,过点B的切线与AD的延长线交于点C.已知∠C=40°,则∠DBA的度数是40°.  全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:初中数学 来源: 题型:解答题
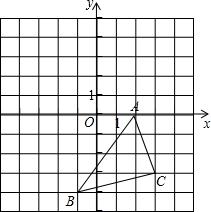 在如图所示的直角坐标系中,解答下列问题:
在如图所示的直角坐标系中,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
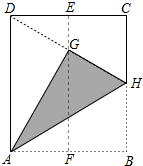 如图,在一张矩形纸片ABCD中,AD=4cm,点E,F分别是CD和AB的中点,现将这张纸片折叠,使点B落在EF上的点G处,折痕为AH,若HG延长线恰好经过点D,则CD的长为2$\sqrt{3}$cm.
如图,在一张矩形纸片ABCD中,AD=4cm,点E,F分别是CD和AB的中点,现将这张纸片折叠,使点B落在EF上的点G处,折痕为AH,若HG延长线恰好经过点D,则CD的长为2$\sqrt{3}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 姓名 | 语文 | 数学 | 英语 | 政治 | 历史 |
| 小馨 | 86 | 98 | 100 | 96 | 97 |
| 小霏 | 88 | 99 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
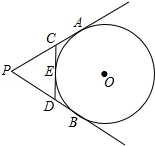 如图,PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D.若⊙O的半径为r,△PCD的周长等于3r,则sin∠APB的值是$\frac{12}{13}$.
如图,PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D.若⊙O的半径为r,△PCD的周长等于3r,则sin∠APB的值是$\frac{12}{13}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com