
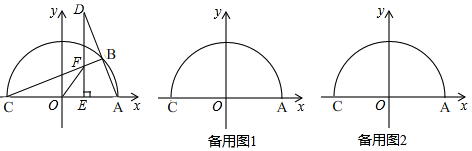
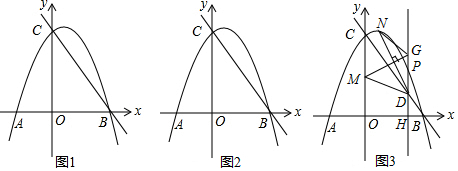
分析 (1)连接OB,由已知得∠AOB=2∠ACB=60°,根据弧长公式求解;
(2)连接CD,由垂直平分线的性质得CD=AB=10,又DE=8,在Rt△CDE中,由勾股定理求CE,依题意证明△CEF∽△DEA,利用相似比求EF;
(3)存在.当以点E、O、F为顶点的三角形与△ABC相似时,分为两种情况:①当交点E在O,B之间时;②当点E在O点的左侧时;分别求E点坐标.
解答 解:(1)∵∠ACB=30°,
∴∠AOB=60°,
∴$\widehat{AB}$=$\frac{60π×5}{180}$=$\frac{5}{3}$π
(2)如图,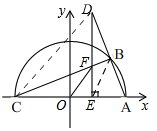
连接CD,
∵∠ACB=90°,BD=BA,
∴CD=CB=10,
∵DE⊥AC,
∴CE=$\sqrt{C{D}^{2}-D{E}^{2}}$=6,
∴AE=AC-CE=4,
∴DE=2AE,
∵∠DFB=∠DAE,∠DFB=∠CFE,
∴∠CFE=∠DAE,
∵∠CEF=∠DEA=90°,
∴△CEF∽△DEA,
∴$\frac{CE}{EF}=\frac{DE}{AE}$=2,
∴EF=$\frac{1}{2}$CE=3;
(3)连接EB,设E(x,0),
当$\widehat{AB}$的度数为60°时,点E恰好与原点O重合;
①0°<$\widehat{AB}$的度数<60°时,点E在O、A之间,∠EOF>∠ACB=∠ADE,
必须令∠EOF=∠EAD,此时有△EOF∽△EAD,
∴$\frac{OE}{AE}=\frac{OF}{AD}$
∵EB是Rt△ADE斜边的中线,
∵BE=AB,
∴∠BEA=∠EAD,
∴∠EOF=∠BEA,
∴OF∥BE,
$\frac{OC}{CE}=\frac{OF}{BE}=\frac{2OF}{AD}$
∴$\frac{OC}{CE}=\frac{2OE}{AE}$,
即$\frac{5}{5+x}=\frac{2x}{5-x}$,
解得x=$\frac{-15±5\sqrt{17}}{4}$,
∵x>0,
∴x=$\frac{-15+5\sqrt{17}}{4}$,
②60°<$\widehat{AB}$的度数<90°时,点E在O点的左侧,
若∠EOF=∠B,则OF∥AD,
∴OF=$\frac{1}{2}$AB=$\frac{1}{4}$AD,
∴$\frac{OF}{AD}=\frac{OE}{AE}=\frac{1}{4}$,
即$\frac{-x}{5-x}=\frac{1}{4}$,解得x=-$\frac{5}{3}$,
若∠EOF=∠ACB,则x=-$\frac{5}{2}$,
综上,点E的坐标为($\frac{-15+5\sqrt{17}}{4}$,0)、(-$\frac{5}{3}$,0)、(-$\frac{5}{2}$,0)
点评 此题是圆的综合题,主要考查了弧长公式,勾股定理,圆的性质,相似三角形的性质和判定,平行线分线段成比例定理,解本题的关键是分情况讨论计算点E的坐标.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源:2016-2017学年浙江省七年级3月月考数学试卷(解析版) 题型:填空题
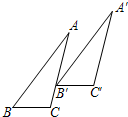
如图,将△ABC平移到△A′B′C′的位置(点B′在AC边上),若∠B=55°,∠C=100°,则∠AB′A′的度数为________________°
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
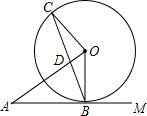 如图,⊙O与射线AM相切于点B,⊙O的半径为3.连结DA,作OC⊥OA交⊙O于点C,连结BC,交DA于点D.
如图,⊙O与射线AM相切于点B,⊙O的半径为3.连结DA,作OC⊥OA交⊙O于点C,连结BC,交DA于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
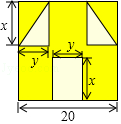 “囧”(jiong)是近时期网络流行语,像一个人脸郁闷的神情.如图所示,一张边长为20的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为x、y,剪去的两个小直角三角形的两直角边长也分别为x、y.
“囧”(jiong)是近时期网络流行语,像一个人脸郁闷的神情.如图所示,一张边长为20的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为x、y,剪去的两个小直角三角形的两直角边长也分别为x、y.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (25%x+10)元 | B. | [(1-25%)x+10]元 | C. | 25%(x+10)元 | D. | (1-25%)(x+10)元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com