
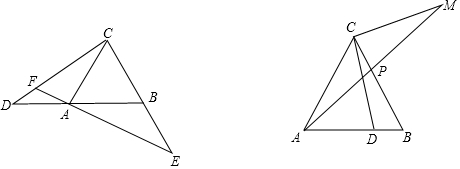
分析 (1)先证明△CAD≌△ABE,推出∠DCA=∠BAE,由∠EAC=∠EFC+∠FCA=∠CAB+∠BAE,推出∠EFC=∠CAB=60°即可解决问题.
(2)如图2中,由题意可知∠FDA=∠FAD=∠EAH=∠AEB=30°,设BH=a则BE=AB=AD=2a,推出DH=2a+2a+a=5a,推出n=$\frac{DH}{BH}$=$\frac{5a}{a}$=5.
(3)如图3中,在BC上截取BN=BD,则AD=CN.想办法证明四边形ACMN是平行四边形即可解决问题.
解答 解:(1)如图1中,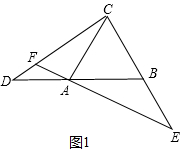
∵△ABC是等边三角形,
∴AB=BC=AC,∠CAB=∠ABC=60°,
∴∠CAD=∠ABE=120°,
在△CAD和△ABE中,
$\left\{\begin{array}{l}{AC=AB}\\{∠CAD=∠ABE}\\{AD=BE}\end{array}\right.$,
∴△CAD≌△ABE,
∴∠DCA=∠BAE,
∵∠EAC=∠EFC+∠FCA=∠CAB+∠BAE,
∴∠EFC=∠CAB=60°,
∴∠DFE=180°-∠CFE=120°.
(2)如图2中,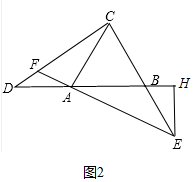
∵△DAF是等腰三角形,∠DFA=120°,
∴∠FDA=∠FAD=∠EAH=∠AEB=30°,设BH=a则BE=AB=AD=2a,
∴DH=2a+2a+a=5a,
∴n=$\frac{DH}{BH}$=$\frac{5a}{a}$=5.
(3)如图3中,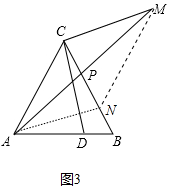
在BC上截取BN=BD,则AD=CN.
在△CAD和△ACN中,
$\left\{\begin{array}{l}{AC=CA}\\{∠ACN=∠CAN}\\{AD=CN}\end{array}\right.$,
∴∠ADC=∠CNA,
∵∠MCN=∠CDA,
∴∠MCN=∠ANC,
∴MC∥AN,
在△MCN和△CDA中,
$\left\{\begin{array}{l}{MC=CD}\\{∠MCN=∠CDA}\\{CN=AD}\end{array}\right.$,
∴△MCN≌△CDA,
∴MN=AC,∠CNM=∠DAC=∠ACN,
∴AC∥MN,
∴四边形ACMN是平行四边形,
∴PC=PN,
∵AD=3BD,AD=CN,BD=BN,
∴CN=3BN,
∴CP:PB=3:5,
故答案为3:5.
点评 本题考查全等三角形的判定和性质、等边三角形的性质、平行四边形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线构造全等三角形,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
 如图,网格中每个小正方形的边长均为1,线段AB、线段EF的端点均在小正方形的顶点上.
如图,网格中每个小正方形的边长均为1,线段AB、线段EF的端点均在小正方形的顶点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
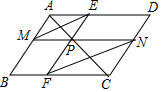 如图,P是平行四边形ABCD的对角线AC上的任一点,过点P的两直线EF、MN与平行四边形ABCD的边分别交于E、F、M、N,求证:ME∥FN.
如图,P是平行四边形ABCD的对角线AC上的任一点,过点P的两直线EF、MN与平行四边形ABCD的边分别交于E、F、M、N,求证:ME∥FN.查看答案和解析>>
科目:初中数学 来源:2016-2017学年浙江省七年级3月月考数学试卷(解析版) 题型:解答题
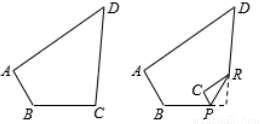
如图是四边形纸片ABCD,其中∠B=120°,∠D=50°。若将其右下角向内折出一∠PCR,恰使CP//AB,RC //AD,如右图所示,求∠C的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com