
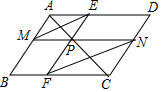
 如图,P是平行四边形ABCD的对角线AC上的任一点,过点P的两直线EF、MN与平行四边形ABCD的边分别交于E、F、M、N,求证:ME∥FN.
如图,P是平行四边形ABCD的对角线AC上的任一点,过点P的两直线EF、MN与平行四边形ABCD的边分别交于E、F、M、N,求证:ME∥FN. 分析 先根据平行四边形的对边平行得出AB∥CD,AD∥BC,利用平行线的性质得出∠AMP=∠CNP,∠MAP=∠NCP,那么△APM∽△CPN,根据相似三角形的性质得出$\frac{AP}{CP}$=$\frac{PM}{PN}$.同理$\frac{AP}{CP}$=$\frac{PE}{PF}$,等量代换得到$\frac{PM}{PN}$=$\frac{PE}{PF}$,又∠MPE=∠NPF,那么△MPE∽△NPF,于是∠PEM=∠PFN,再根据平行线的判定得出ME∥FN.
解答 证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠AMP=∠CNP,∠MAP=∠NCP,
∴△APM∽△CPN,
∴$\frac{AP}{CP}$=$\frac{PM}{PN}$.
同理,∴△APE∽△CPF,
∴$\frac{AP}{CP}$=$\frac{PE}{PF}$,
∴$\frac{PM}{PN}$=$\frac{PE}{PF}$,
又∠MPE=∠NPF,
∴△MPE∽△NPF,
∴∠PEM=∠PFN,
∴ME∥FN.
点评 本题考查了平行四边形的性质,相似三角形的判定与性质,平行线的判定与性质,难度适中.得出$\frac{PM}{PN}$=$\frac{PE}{PF}$是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省苏州太仓市第二学期初一期中模拟数学试卷(解析版) 题型:解答题
因式分【解析】
(1) x2﹣36;
(2) xy2﹣x;
(3) ab4﹣4ab3+4ab2;
(4) (m+1)(m﹣9)+8m.
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省苏州太仓市第二学期初一期中模拟数学试卷(解析版) 题型:选择题
把多项式5x3﹣5x进行因式分解正确的结果是( )
A.5x3﹣5x=5(x3﹣x)
B.5x3﹣5x=5x(x2﹣1)
C.5x3﹣5x=5x(x+1)(x﹣1)
D.5x3﹣5x=5x2(1+ )(x﹣1)
)(x﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
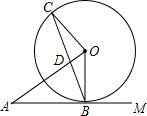 如图,⊙O与射线AM相切于点B,⊙O的半径为3.连结DA,作OC⊥OA交⊙O于点C,连结BC,交DA于点D.
如图,⊙O与射线AM相切于点B,⊙O的半径为3.连结DA,作OC⊥OA交⊙O于点C,连结BC,交DA于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com