
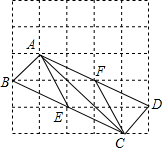
 如图,在由边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,E为BC中点,AD∥BC(D为格点),请按要求完成下列各题:
如图,在由边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,E为BC中点,AD∥BC(D为格点),请按要求完成下列各题:分析 (1)由勾股定理得出AB2+AC2=BC2,由勾股定理的逆定理即可得出△ABC是直角三角形;
(2)由勾股定理求出AD、AE、CE、CF,得出AF,AE=CE=CF=AF,由菱形的判定定理即可得出结论..
解答 (1)证明:由勾股定理得:
AB2=12+12=2,AC2=32+32=18,BC2=42+22=20,
∴AB2+AC2=BC2,
∴△ABC是直角三角形;
(2)解:四边形AECF是菱形;理由如下:
由勾股定理得:AD=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,AE=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
CE=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,CF=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
∵F为AD中点,
∴AF=$\frac{1}{2}$AD=$\sqrt{5}$,
∴AE=CE=CF=AF,
∴四边形AECF是菱形.
点评 本题考查了勾股定理、勾股定理的逆定理、菱形的判定定理;熟练掌握勾股定理,由勾股定理求出有关线段的长度得出数量关系是解决问题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在端午节来临之际,某店购进两种品牌的盒装粽子,购进乙品牌盒装粽子的数量y(盒)与甲品牌盒装粽子的数量x(盒)之间的函数关系如图所示:
在端午节来临之际,某店购进两种品牌的盒装粽子,购进乙品牌盒装粽子的数量y(盒)与甲品牌盒装粽子的数量x(盒)之间的函数关系如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 平时成绩 | 期中成绩 | 期末成绩 | |
| 小张 | 82 | 85 | 91 |
| 小王 | 84 | 89 | 86 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com