
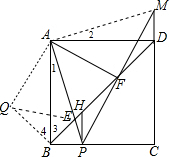
 如图,正方形ABCD中,点P是边BC上一点,PH⊥BC交BD于点H,连接AP交BD于点E,点F为DH中点,PF交CD的延长线于点M,连接AF.
如图,正方形ABCD中,点P是边BC上一点,PH⊥BC交BD于点H,连接AP交BD于点E,点F为DH中点,PF交CD的延长线于点M,连接AF.
|
|
|


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
| (k-2)•180° |
| k |

查看答案和解析>>
科目:初中数学 来源: 题型:
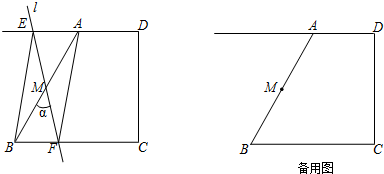
查看答案和解析>>
科目:初中数学 来源: 题型:
 某社区准备在甲、乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同,小宇根据他们的成绩绘制了如图尚不完整的统计图表,并计算了甲成绩的平均数和方差(见小宇的作业).
某社区准备在甲、乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同,小宇根据他们的成绩绘制了如图尚不完整的统计图表,并计算了甲成绩的平均数和方差(见小宇的作业).| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
| 甲成绩 | 9 | 4 | 7 | 4 | 6 |
| 乙成绩 | 7 | 5 | 7 | a | 7 |
. |
| x乙 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
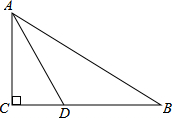 如图,在Rt△ABC中,∠B=90°,AD平分∠BAC,∠BAD=α,sinα=
如图,在Rt△ABC中,∠B=90°,AD平分∠BAC,∠BAD=α,sinα=
| ||
| 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com