
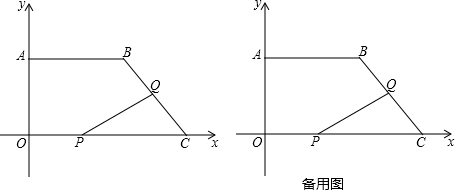
���� ��1����B������BH��OC����Rt��BHC������BH=4$\sqrt{3}$��CH=4���õ���B�����ꣻ
��2�����ݵ㲻ͬʱ���Q���λ�ã���0��t��8��8��t��12���ֱ�����OPQ�����S��ʱ��t֮��ĺ�����ϵʽ��
��3���������ۣ��ù��ɶ�����ʾ�߶Σ��з�����⣮
��� �⣺��1����BH��OC������ΪH����Rt��BHC�У�
��BC=8����C=60�㣬
��BH=4$\sqrt{3}$��CH=4��
��OC=12��
��OH=8
��B��8��4$\sqrt{3}$����
��2����0��t��8ʱ����QM��OC��
��Rt��CQM��
�ߡ�C=60�㣬
���CQM=30�㣬
��CM=$\frac{1}{2}$CQ=$\frac{t}{2}$��QM=$\frac{\sqrt{3}t}{2}$��
��S��OPQ=$\frac{1}{2}$•OP•QM=$\frac{\sqrt{3}{t}^{2}}{4}$��
��8��t��12ʱ��S��OPQ=$\frac{1}{2}$•OP•BH=2$\sqrt{3}$t��
��3����Q����BC���ϣ�
��0��t��8
��O��0��0����P��t��0����Q��12-$\frac{t}{2}$��$\frac{\sqrt{3}t}{2}$����
����OP=OQ����OP2=OQ2��OP2=t2��OQ2=��12-$\frac{t}{2}$��2+��$\frac{\sqrt{3}t}{2}$��2
����t2=��12-$\frac{t}{2}$��2+��$\frac{\sqrt{3}t}{2}$��2
��ã�t=12��8���������⣬��ȥ��
����PO=PQ����OP2=PQ2��OP2=t2��PQ2=��12-$\frac{t}{2}$-t��2+��$\frac{\sqrt{3}t}{2}$��2
����t2=��12-$\frac{t}{2}$-t��2+��$\frac{\sqrt{3}t}{2}$��2
��ã�t1=6��t2=12������ȥ����
����QO=QP����OQ2=PQ2��PQ2=��12-$\frac{t}{2}$-t��2+��$\frac{\sqrt{3}t}{2}$��2��OQ2=��12-$\frac{t}{2}$��2+��$\frac{\sqrt{3}t}{2}$��2
������12-$\frac{t}{2}$-t��2+��$\frac{\sqrt{3}t}{2}$��2=��12-$\frac{t}{2}$��2+��$\frac{\sqrt{3}t}{2}$��2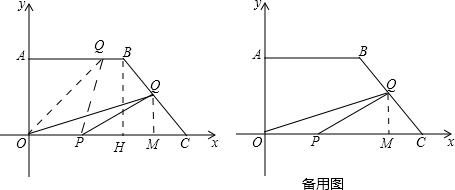
��ã�t1=0����ȥ����t2=12����ȥ����
������������t=6ʱ����OPQΪ���������Σ�
���� ������Ҫ�����˶������⣬�������ۣ����ɶ�������������Լ����������ε��ж������ʣ������ܵ�˼��������������ν���ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ��ֱ��AB��CD�ཻ�ڵ�O����DOE����BOD=3��2��OFƽ�֡�AOE������AOC=24�㣬���EOF�Ķ�����
��ͼ��ʾ��ֱ��AB��CD�ཻ�ڵ�O����DOE����BOD=3��2��OFƽ�֡�AOE������AOC=24�㣬���EOF�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
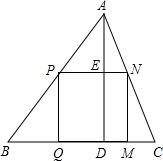 ��ͼ����ABCΪһ��������Σ�BC=12��BC���ϵĸ�AD=8����Q��M�ڱ�BC�ϣ�P��N�ֱ��ڱ�AB��AC�ϣ���PNMQΪ���Σ�
��ͼ����ABCΪһ��������Σ�BC=12��BC���ϵĸ�AD=8����Q��M�ڱ�BC�ϣ�P��N�ֱ��ڱ�AB��AC�ϣ���PNMQΪ���Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
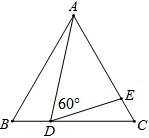 ��֪����ͼ����ABC�ǵȱ������Σ���D��E�ֱ��ڱ�BC��AC�ϣ���ADE=60�㣮
��֪����ͼ����ABC�ǵȱ������Σ���D��E�ֱ��ڱ�BC��AC�ϣ���ADE=60�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
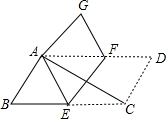 ��ͼ����ƽ���ı���ABCDֽƬ��EF�۵���ʹ��C���A�غϣ���D���ڵ�G����
��ͼ����ƽ���ı���ABCDֽƬ��EF�۵���ʹ��C���A�غϣ���D���ڵ�G�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com