
分析 (1)根据正方形和长方形的周长公式即可求解;
(2)利用完全平方公式即可求解;
(3)根据长方形面积公式,利用面积除以边长即可求解;
(4)根据周长公式求得两个图形周长公式求解,即可比较.
解答 解:(1)S=a2+b2+2ab.故答案是:a2+b2+2ab;
(2)S=a2+b2+2ab=(a+b)2.
故答案是:a+b;
(3)宽是:$\frac{(\\;a+\\;b)^{2}}{2(\\;a+\\;b)}$=$\frac{1}{2}$(a+b);
(4)M的周长是4(a+b),
N的周长是2×$\frac{1}{2}$(a+b)+2×【2(a+b)】=a+b+4a+4b=5(a+b),
则N的周长较大.
点评 本题考查了完全平方公式和正方形、长方形的面积与周长的计算,正确理解完全平方公式是关键.


科目:初中数学 来源: 题型:填空题
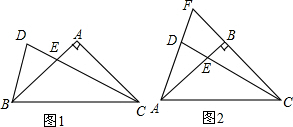
 如图,若∠B=40°,A、C分别为角两边上的任意一点,连接AC,∠BAC与∠ACB的平分线交于点P1,则∠P1=110°,D、F也为角两边上的任意一点,连接DF,∠BFD与∠FDB的平分线交于点P2,…按这样规律,则∠P2016=110°.
如图,若∠B=40°,A、C分别为角两边上的任意一点,连接AC,∠BAC与∠ACB的平分线交于点P1,则∠P1=110°,D、F也为角两边上的任意一点,连接DF,∠BFD与∠FDB的平分线交于点P2,…按这样规律,则∠P2016=110°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
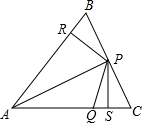 如图,△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S,若AQ=PQ,PR=PS,下面四个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP;④AP垂直平分RS.其中正确结论的序号是①②④(请将所有正确结论的序号都填上).
如图,△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S,若AQ=PQ,PR=PS,下面四个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP;④AP垂直平分RS.其中正确结论的序号是①②④(请将所有正确结论的序号都填上).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
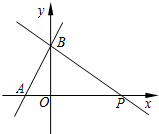 如图,一次函数y=(m+1)x+$\frac{3}{2}$的图象与x轴的负半轴相交于点A,与y轴相交于点B,且△OAB面积为$\frac{3}{4}$.
如图,一次函数y=(m+1)x+$\frac{3}{2}$的图象与x轴的负半轴相交于点A,与y轴相交于点B,且△OAB面积为$\frac{3}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com