
 某露天游泳池对外开放时,收入以出售门票的方式获得,每天各项开支的总成本是固定的,一天内盈利y(元)与购票进场的人数x(人)之间的函数关系如图所示.为保证游泳时的安全与卫生,管理部门对每天进入游泳池的人数进行了限制.
某露天游泳池对外开放时,收入以出售门票的方式获得,每天各项开支的总成本是固定的,一天内盈利y(元)与购票进场的人数x(人)之间的函数关系如图所示.为保证游泳时的安全与卫生,管理部门对每天进入游泳池的人数进行了限制.

科目:初中数学 来源: 题型:
 探索规律:观察如图由“※”组成的图案和算式,解答问题:
探索规律:观察如图由“※”组成的图案和算式,解答问题:查看答案和解析>>
科目:初中数学 来源: 题型:
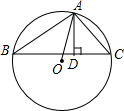 如图,已知△ABC内接于⊙O,AD为BC边上的高.
如图,已知△ABC内接于⊙O,AD为BC边上的高.查看答案和解析>>
科目:初中数学 来源: 题型:
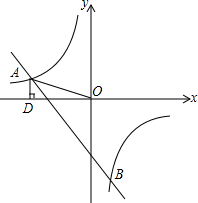 如图,一次函数y=kx+b的图象与反比例函数y=
如图,一次函数y=kx+b的图象与反比例函数y=| m |
| x |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在每个小正方形的边长均为1个单位长度的方格纸中,有一个△ABC,△ABC的三个顶点均与小正方形的顶点重合.
如图,在每个小正方形的边长均为1个单位长度的方格纸中,有一个△ABC,△ABC的三个顶点均与小正方形的顶点重合.查看答案和解析>>
科目:初中数学 来源: 题型:
A、2
| ||
B、2<r<2
| ||
| C、2<r<3 | ||
| D、3<r<4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,点M在射线OA上,点N在射线OB上,芳芳在直线MN上求作一点P,使它到OA、OB的距离相等,则点P是( )
如图,点M在射线OA上,点N在射线OB上,芳芳在直线MN上求作一点P,使它到OA、OB的距离相等,则点P是( )| A、线段MN的中点 |
| B、OA与OB的中垂线的交点 |
| C、OA与MN的中垂线的交点 |
| D、MN与∠AOB的平分线的交点 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com