Question

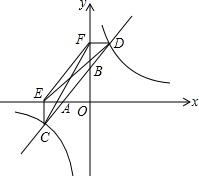
如图，一次函数y=kx+b的图象与x轴、y轴交于A、B两点，与反比例函数的图象相交于C、D两点，分别过点C、D作x轴、y轴的垂线，垂足为E、F，连接CF，DE．下列四个结论中：
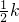①△CEF的面积等于；②△DCE≌△CDF；③四边形ADFE是平行四边形；④AC=BD．　 正确的结论是________．（填正确结论的序号）

Answer 1

①③④
分析：点P为CE、DF的延长线的交点，CM⊥y轴于M，DN⊥x轴于N，根据反比例函数的比例系数的几何意义得到S_矩形ECMO=CM•CE=k，S_矩形FDNO=FD•DN=k，则S_△CEF=EC•FP=k；也有CM•CE=FD•DN，用DN=PE代换后变形得到PF：FD=PE：EC，根据平行线分线段成比例定理的逆定理得EF∥CD，易得四边形AEFD为平行四边形；则DF=AE，所以EC≠FD，由此判断四边形ECDF不是等腰梯形，△DCE与△CDF不全等；然后根据“ASA”证明△FDB≌△EAC，则有BD=AC．
解答：点P为CE、DF的延长线的交点，CM⊥y轴于M，DN⊥x轴于N，如图，
∵点C、D都在y=的图象上，
∴S_矩形ECMO=CM•CE=k，S_矩形FDNO=FD•DN=k，
∴S_△CEF=EC•FP，
∵CE⊥x轴，DF⊥y轴，
∴CM=FP，
∴S_△CEF=k，所以①正确；
∴CM•CE=FD•DN，
而DN=PE，
∴PF•CE=FD•PE，即PF：FD=PE：EC，
∴EF∥CD，
∵FD∥AE，
∴四边形AEFD为平行四边形，所以③正确；
∴DF=AE，
∴EC≠FD，
∴四边形ECDF不是等腰梯形，
∴△DCE与△CDF不全等，所以②错误；
∵DF∥AE，
∴∠FDB=∠EAC，
在△FDB和△EAC中
，
∴△FDB≌△EAC，
∴BD=AC，所以④正确．
故答案为①③④．
点评：本题考查了反比例函数的综合题：掌握反比例函数图象上点的坐标特征、比例系数的几何意义和平行四边形的判定与性质．