
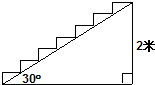
 如图,在高为2m,坡角为30°的楼梯表面铺地毯,地毯的长度至少需要( )
如图,在高为2m,坡角为30°的楼梯表面铺地毯,地毯的长度至少需要( )| A. | 2($\sqrt{3}$+1)m | B. | 4m | C. | ($\sqrt{3}$+2)m | D. | 2($\sqrt{3}$+3)m |
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
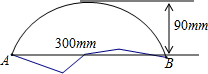 一支考古队发现一个残破的古代圆盘碎片,如图所示,考古家测量了弦AB=300mm,圆弧的高为90mm,于是得到了古圆盘的半径,从而确定了它的圆心,终于使这个古物得以复原,请问你知道考古家怎样得到它的半径吗?
一支考古队发现一个残破的古代圆盘碎片,如图所示,考古家测量了弦AB=300mm,圆弧的高为90mm,于是得到了古圆盘的半径,从而确定了它的圆心,终于使这个古物得以复原,请问你知道考古家怎样得到它的半径吗?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
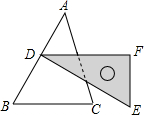 如图,含30°角的直角三角尺DEF放置在△ABC上,30°角的顶点D在边AB上,DE⊥AB,且BC∥DF.若∠A=50°,则∠C的度数为70°.
如图,含30°角的直角三角尺DEF放置在△ABC上,30°角的顶点D在边AB上,DE⊥AB,且BC∥DF.若∠A=50°,则∠C的度数为70°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com