
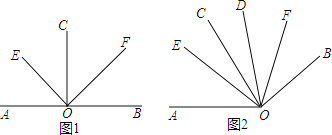
【题目】(1)如图1,若CO⊥AB,垂足为O,OE、OF分别平分∠AOC与∠BOC.求∠EOF的度数;
(2)如图2,若∠AOC=∠BOD=80°,OE、OF分别平分∠AOD与∠BOC.求∠EOF的度数;
(3)若∠AOC=∠BOD=α,将∠BOD绕点O旋转,使得射线OC与射线OD的夹角为β,OE、OF分别平分∠AOD与∠BOC.若α+β≤180°,α>β,则∠EOC= .(用含α与β的代数式表示)
【答案】(1)90°;(2)80°;(3)![]()
【解析】
试题分析:(1)根据垂直的定义得到∠AOC=∠BOC=90°,根据角平分线的定义即可得到结论;
(2)根据角平分线的定义得到∠EOD=![]() ∠AOD=
∠AOD=![]() ×(80+β)=40+
×(80+β)=40+![]() β,∠COF=
β,∠COF=![]() ∠BOC=
∠BOC=![]() ×(80+β)=40+
×(80+β)=40+![]() β,根据角的和差即可得到结论;
β,根据角的和差即可得到结论;
(3)如图2由已知条件得到∠AOD=α+β,根据角平分线的定义得到∠DOE=![]() (α+β),即可得到结论.
(α+β),即可得到结论.
解:(1)∵CO⊥AB,
∴∠AOC=∠BOC=90°,
∵OE平分∠AOC,
∴∠EOC=![]() ∠AOC=
∠AOC=![]() ×90°=45°,
×90°=45°,
∵OF平分∠BOC,
∴∠COF=![]() ∠BOC=
∠BOC=![]() ×90°=45°,
×90°=45°,
∠EOF=∠EOC+∠COF=45°+45°=90°;
(2)∵OE平分∠AOD,
∴∠EOD=![]() ∠AOD=
∠AOD=![]() ×(80+β)=40+
×(80+β)=40+![]() β,
β,
∵OF平分∠BOC,
∴∠COF=![]() ∠BOC=
∠BOC=![]() ×(80+β)=40+
×(80+β)=40+![]() β,
β,
∠COE=∠EOD﹣∠COD=40+![]() β﹣β=40﹣
β﹣β=40﹣![]() β;
β;
∠EOF=∠COE+∠COF=40﹣![]() β+40+
β+40+![]() β=80°;
β=80°;
(3)如图2,∵∠AOC=∠BOD=α,∠COD=β,
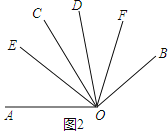
∴∠AOD=α+β,
∵OE平分∠AOD,
∴∠DOE=![]() (α+β),
(α+β),
∴∠COE=∠DOE﹣∠COD=![]() =
=![]() ,
,
如图3,∵∠AOC=∠BOD=α,∠COD=β,
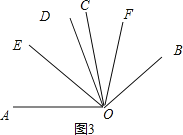
∴∠AOD=α+β,
∵OE平分∠AOD,
∴∠DOE=![]() (α﹣β),
(α﹣β),
∴∠COE=∠DOE+∠COD=![]() .
.
综上所述:![]() ,
,
故答案为:![]() .
.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】将正整数1,2,3,4……按以下方式排列
1 4 → 5 8 → 912 → ……
↓ ↑ ↓ ↑ ↓ ↑
2 → 36 → 7 10 → 11
根据排列规律,从2010到2012的箭头依次为
A.↓ → B.→ ↓ C.↑ → D. → ↑
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】E、F、G、H分别是四边形ABCD四条边的中点,要使四边形EFGH为矩形,四边形ABCD应具备的条件是( )
A、对角线相等
B、一组对边平行而另一组对边不平行
C、对角线互相垂直
D、对角线互相平分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a为最小的正整数,b是最大的负整数,c是绝对值最小的数,d是倒数等于自身的有理数,则a﹣b+c﹣d的值为( )
A 1 B.3 C.1或3 D.2或﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列数阵是由偶数排列而成的:
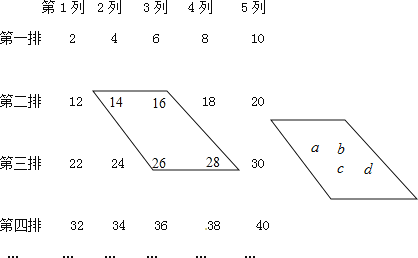
(1)在数阵中任意作一类似的框,如果这四个数的和为188,能否求出这四个数?如果能,求出这些数,如果不能,说明理由.如果和为288,能否求出这四个数?说明理由.
(2)有理数110在上面数阵中的第 排、第 列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com