练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．如图，以数轴为单位长度线段为边作一个正方形，以表示数2的点为圆心，正方形对角线长为半径画弧，交数轴于点A，则点A表示的数是2-$\sqrt{2}$．

    分析 根据题意利用勾股定理得出BD的长，再利用AD=DB得出A点位置，即可得出答案．

    解答 解：由题意可得：
    ∵BC=CD=1，
    ∴BD=$\sqrt{2}$，
    故AD=$\sqrt{2}$，
    则点A表示的数是：2-$\sqrt{2}$．
    故答案为：2-$\sqrt{2}$．

    点评 此题主要考查了勾股定理以及正方形的性质，正确应用勾股定理是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017届四川省遂宁市九年级上学期期末考试数学试卷（解析版） 题型：单选题

    在平面直角坐标系中，已知点O（0，0），A（2，4）.将线段OA沿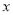 轴向左平移2个单位，记点O，A的对应点分别为点O1，A1，则点O1，A1的坐标分别是 （ ）

    A. （0，0），（2，4） B. （0，0），（0，4）

    C. （2，0），（4，4） D. （－2，0），（0，4）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．若a+b＞0，ab＜0，则（　　）
    A．a、b异号，且|a|＞|b|B．a、b异号，且|a|＜|b|
    C．a、b异号，且|a|=|b|D．a、b异号，且正数的绝对值较大

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．在△ABC中，∠A、∠B都为锐角，且|sinA-$\frac{1}{2}$|+（$\frac{\sqrt{2}}{2}$-cosB）2=0，求∠C的度数105°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．下列各组数，能构成直角三角形的是（　　）
    A．4，5，6B．8，15，17C．5，10，13D．8，39，40

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．观察下列一组等式，然后解答后面的问题：
    （$\sqrt{2}+1$）（$\sqrt{2}-1$）=1，（$\sqrt{3}+\sqrt{2}$）（$\sqrt{3}-\sqrt{2}$）=1，（$\sqrt{4}+\sqrt{3}$）（$\sqrt{4}-\sqrt{3}$）=1，（$\sqrt{5}+\sqrt{4}$）（$\sqrt{5}-\sqrt{4}$）=1…
    （1）观察上面的规律，计算下列式子的值：
    （$\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{2013}+\sqrt{2012}}$）（$\sqrt{2013}+1$）．
    （2）利用上面的规律，试比较$\sqrt{12}-\sqrt{11}$与$\sqrt{13}-\sqrt{12}$的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．在数轴上表示数：0.5，-|-2|，-（-3），-4，22，按从小到大的顺序用“＜”连接起来．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．2015年8月6日美国太空总署发放一套影像，由卫星拍摄月球围绕地球转动时，其反面在被太阳光照亮的情况下，横越过太平洋需数小时．若该天月球横越太平洋前的表面温度为-165℃，横越太平洋后，月球的表面温度上升了247℃，则横越太平洋后月球的表面温度为（　　）
    A．82℃B．-82℃C．412℃D．247℃

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．已知m为实数，若（m2+4m）2+5（m2+4m）-24=0，则m2+4m的值为3．

    查看答案和解析>>

    同步练习册答案