
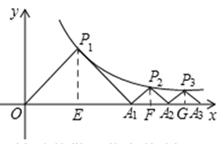
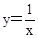 (x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn﹣1An都是等腰直角三角形,斜边OA1,A1A2,A2A3,…,An﹣1An都在x轴上(n是大于或等于2的正整数),则点P3的坐标是 ;点Pn的坐标是 (用含n的式子表示).
(x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn﹣1An都是等腰直角三角形,斜边OA1,A1A2,A2A3,…,An﹣1An都在x轴上(n是大于或等于2的正整数),则点P3的坐标是 ;点Pn的坐标是 (用含n的式子表示).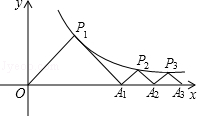
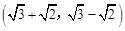 ;
;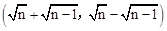 。
。
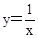 ,可得a=1。
,可得a=1。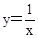 ,可得b=
,可得b=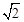 ﹣1,
﹣1,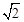 +1,
+1,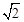 ﹣1)。∴A1F=A2F=2
﹣1)。∴A1F=A2F=2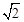 ﹣2,OA2=OA1+A1A2=2
﹣2,OA2=OA1+A1A2=2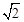 。
。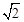 ,c),将点P1(c+2
,c),将点P1(c+2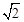 ,c)代入y=,可得c=
,c)代入y=,可得c=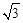 ﹣
﹣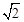 。
。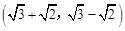
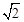 +1,
+1,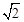 ﹣1),P3的坐标为
﹣1),P3的坐标为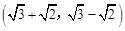 b。
b。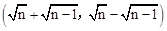 。
。

科目:初中数学 来源:不详 题型:解答题
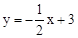 交AB,BC分别于点M,N,反比例函数
交AB,BC分别于点M,N,反比例函数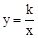 的图象经过点M,N.
的图象经过点M,N.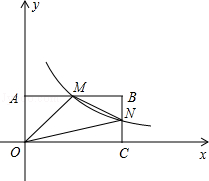
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
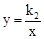 的图象在第一象限交于点C,CD⊥x轴,垂足为D,OB是△ACD的中位线。
的图象在第一象限交于点C,CD⊥x轴,垂足为D,OB是△ACD的中位线。
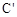 是点C关于y轴的对称点,请求出△
是点C关于y轴的对称点,请求出△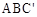 的面积。
的面积。查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 (x>
(x> )图象上一点P,PA⊥x轴于点A(a,0),点B坐标为(0,b)(b>0),动点M是y轴正半轴上B点上方的点,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q,连结AQ,取AQ的中点为C.
)图象上一点P,PA⊥x轴于点A(a,0),点B坐标为(0,b)(b>0),动点M是y轴正半轴上B点上方的点,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q,连结AQ,取AQ的中点为C.
 ,求此时P点的坐标;
,求此时P点的坐标;查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 在第一象限内的图象上的一个点,以点P为顶点作等边△PAB,使A、B落在x轴上,则△POA的面积是
在第一象限内的图象上的一个点,以点P为顶点作等边△PAB,使A、B落在x轴上,则△POA的面积是
 D.
D.
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
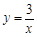 ,
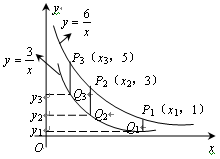
,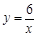 在第一象限内的图像如图所示,点
在第一象限内的图像如图所示,点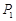 ,
,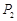 ,
,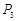 ,…,
,…,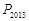 在函数
在函数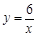 的图像上,它们的横坐标分别是
的图像上,它们的横坐标分别是 ,
,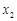 ,
,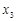 ,…,
,…,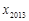 ,纵坐标分别是1,3,5,…,共2013个连续奇数,过点
,纵坐标分别是1,3,5,…,共2013个连续奇数,过点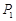 ,
,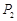 ,
,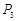 ,…,
,…,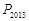 分别作y轴的平行线,与函数
分别作y轴的平行线,与函数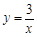 的图像交点依次是
的图像交点依次是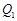 (
( ,
,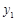 ),
), (
(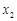 ,
,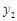 ),
),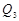 (
(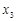 ,
,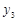 ),…,
),…,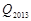 (
(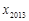 ,
,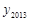 ),则
),则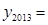 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com