

���� ��1�����������֪��sad60��Ϊ����Ϊ60��ĵ��������ε����ԣ��Ӷ��������sad60���ֵ��
��2������Rt��ABC�У���C=90�㣬sinA=$\frac{3}{5}$�������ԡ�AΪ���ǵĵ��������Σ�Ȼ�����������Խ���⣮
��3���ٽ��ۣ�PC��x�ᣬֻҪ֤����OAB=��PCE���ɣ�
����ͼ4�У��ֱ��������C��AB�е�ʱ����P�����ꣻ����C����B�غ�ʱ����P��ĺ����꣬���ɽ�����⣮
��� ��1���߶���Ϊ60��ĵ����������ǵȱ������Σ�
��sad60��=$\frac{�ױ�}{��}$=$\frac{1}{1}$=1��
�ʴ�Ϊ��1��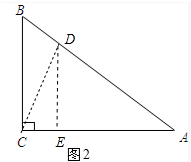
��2����ͼ2�У���AB=5a��BC=3a����AC=4a����AB�Ͻ�ȡAD=AC=4a����DE��AC�ڵ�E��
��Rt��ABC�У���C=90�㣬sinA=$\frac{3}{5}$��
��DE=AD•sinA=4a��$\frac{3}{5}$=$\frac{12}{5}$a��AE=AD•cosA=4a��$\frac{4}{5}$=$\frac{16}{5}$a��
��CE=AC-AE=4a-$\frac{16}{5}$a=$\frac{4}{5}$a��
��CD=$\sqrt{C{E}^{2}+E{D}^{2}}$=$\sqrt{��\frac{4}{5}a��^{2}+��\frac{12}{5}a��^{2}}$=$\frac{4\sqrt{10}}{5}$a����
��sadA=$\frac{CD}{AC}$=$\frac{\frac{4\sqrt{10}}{5}a}{4a}$=$\frac{\sqrt{10}}{5}$��
��sadA=$\frac{\sqrt{10}}{5}$��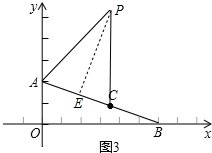
��3���ٽ��ۣ�PC��x�ᣬ
���ɣ���ͼ3�У���PE��AC��E��
��PA=PC��
��AE=EC��
��sadAPC=$\frac{AC}{PC}$=$\frac{2}{3}$��
��$\frac{2EC}{PC}$=$\frac{2}{3}$��
��cos��PCE=$\frac{EC}{PC}$=$\frac{1}{3}$��
��Rt��AOB�У��ߡ�AOB=90�㣬OA=2��OB=4$\sqrt{2}$��
��AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{2}^{2}��4\sqrt{2}��^{2}}$=6��
��cos��OAB=$\frac{OA}{AB}$=$\frac{2}{6}$=$\frac{1}{3}$��
��cos��PCE=cos��OAB��
���OAB=��PCE��
��PC��y�ᣬ
��PC��x�ᣮ
����ͼ4�У�����C��AB�е�ʱ����PE��AB��E����x����M����PN��x����N��
��sad��APC=$\frac{AC}{PC}$=$\frac{2EC}{PC}$=$\frac{4\sqrt{2}}{3}$��
��$\frac{1.5}{PC}$=$\frac{2\sqrt{2}}{3}$��
��PC=$\frac{9\sqrt{2}}{8}$��PE=$\sqrt{P{C}^{2}-E{C}^{2}}$=$\frac{3\sqrt{2}}{8}$��
�ߡ�EBM=��ABO����MEB=��AOB=90�㣬
���BEM�ס�BOA��
��$\frac{EB}{BO}$=$\frac{EM}{AO}$=$\frac{BM}{AB}$����EMB=��OAB��
��EM=$\frac{7\sqrt{2}}{8}$��BM=$\frac{21\sqrt{2}}{8}$��
��PM=PE+EM=$\frac{5\sqrt{2}}{4}$��OM=OB-MB=$\frac{11\sqrt{2}}{8}$��
�ߡ�PNM=��AOB����PMN=��OAB��
���PNM�ס�BOA��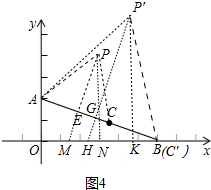
��$\frac{PM}{AB}$=$\frac{MN}{AO}$��
��MN=$\frac{5\sqrt{2}}{12}$��
��ON=$\frac{43\sqrt{2}}{24}$��
���P�ĺ�����Ϊ$\frac{43\sqrt{2}}{24}$��
����C����B�غ�ʱ����P��K��OB��PG��AB��G��OB��H��
��sad��AP��B=$\frac{4\sqrt{2}}{3}$=$\frac{AB}{P��B}$=$\frac{2GB}{P��B}$��
��P��B=$\frac{9\sqrt{2}}{4}$��P��G=$\sqrt{P��{B}^{2}-G{B}^{2}}$=$\frac{3\sqrt{2}}{4}$��
�ɡ�BGH�ס�BOA�õ���$\frac{GH}{AO}$=$\frac{GB}{BO}$=$\frac{BH}{AB}$��
��GH=$\frac{3\sqrt{2}}{4}$��BH=$\frac{9\sqrt{2}}{4}$��OH=$\frac{7\sqrt{2}}{4}$��
��P��H=$\frac{3\sqrt{2}}{2}$��
�ɡ�P��KH�ס�BOA�õ���$\frac{HK}{AO}$=$\frac{P��H}{AB}$��
��HK=$\frac{\sqrt{2}}{2}$��
��OK=$\frac{9\sqrt{2}}{4}$��
���P��ĺ�����Ϊ$\frac{9\sqrt{2}}{4}$��
�൱ sad��APC=$\frac{{4\sqrt{2}}}{3}$ʱ����P�ĺ�����x��ȡֵ��ΧΪ$\frac{43\sqrt{2}}{24}$��x��$\frac{9\sqrt{2}}{4}$��
���� ���⿼���ֱ�������Σ����������ε����ʡ����ɶ��������������ε��ж������ʵ�֪ʶ������Ĺؼ����������¶��壬ѧ�����ӳ��ø����ߣ�����ֱ�������Σ�ѧ�ῼ������λ�ý�����⣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ѡ�ABC��ABƽ�Ƶ���A��B��C���λ�ã����ǵ��ص����ֵ�����ǡ�ABC�����һ�룬��AB=$\sqrt{2}$������������ƶ��ľ���A��A��
��ͼ���ѡ�ABC��ABƽ�Ƶ���A��B��C���λ�ã����ǵ��ص����ֵ�����ǡ�ABC�����һ�룬��AB=$\sqrt{2}$������������ƶ��ľ���A��A���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=x-1 | B�� | y=-x+1 | C�� | y=x+1 | D�� | y=-x-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 60�� | B�� | 120�� | C�� | 30�� | D�� | 150�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������ABCD�Ķ���C��D�ڷ���������y=$\frac{8}{x}$��x��0����ͼ���ϣ�����A��B�ֱ���x���y����������ϣ��������Ҳ���������EFDG������G�ڷ���������y=$\frac{8}{x}$��x��0����ͼ���ϣ�����E��x����������ϣ����G������Ϊ��2$\sqrt{3}$+2��2$\sqrt{3}$-2����
��ͼ��������ABCD�Ķ���C��D�ڷ���������y=$\frac{8}{x}$��x��0����ͼ���ϣ�����A��B�ֱ���x���y����������ϣ��������Ҳ���������EFDG������G�ڷ���������y=$\frac{8}{x}$��x��0����ͼ���ϣ�����E��x����������ϣ����G������Ϊ��2$\sqrt{3}$+2��2$\sqrt{3}$-2�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

| �������֣� | �������ˣ� |
| 68 | 4 |
| 78 | 7 |
| 80 | 3 |
| 88 | 5 |
| 90 | 10 |
| 96 | 6 |
| 100 | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ�������������ABC�У���AB=c��AC=b��BC=a���ӳ�AC����E��ʹCE=a������BE��
��ͼ�������������ABC�У���AB=c��AC=b��BC=a���ӳ�AC����E��ʹCE=a������BE���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com