
已知:如图,在□ EFGH中,点F的坐标是(-2,-1),∠EFG=45°.
(1)求点H的坐标;
(2)抛物线![]() 经过点E、G、H,现将
经过点E、G、H,现将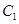 向左平移使之经过点F,得到抛物线
向左平移使之经过点F,得到抛物线 ,求抛物线
,求抛物线![]() 的解析式;
的解析式;
(3)若抛物线![]() 与y轴交于点A,点P在抛物线
与y轴交于点A,点P在抛物线 的对称轴上运动.请问:是否存在以AG为腰的等腰三角形AGP?若存在,求出点P的坐标;若不存在,请说明理由.
的对称轴上运动.请问:是否存在以AG为腰的等腰三角形AGP?若存在,求出点P的坐标;若不存在,请说明理由.
解:(1)∵在□ABCD中
∴EH=FG=2 ,G(0,-1)即OG=1………………………1’
∵∠EFG=45°
∴在Rt△HOG中,∠EHG=45°
可得OH=1
∴H(1,0)……………………………………………………2’
(2)∵OE=EH-OH=1
∴E(-1,0),
设抛物线![]() 解析式为
解析式为![]() =
=![]() +bx+c
+bx+c
∴代入E、G、H三点,
∴![]() =1 ,b=0,,c=-1
=1 ,b=0,,c=-1
∴![]() =
=![]() -1……………………………………………………3’
-1……………………………………………………3’
依题意得,点F为顶点,∴过F点的抛物线 解析式是
解析式是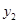 =
=![]() -1…………………4’
-1…………………4’
(3)∵抛物线![]() 与y轴交于点A ∴A(0,3),∴AG=4
与y轴交于点A ∴A(0,3),∴AG=4
情况1:AP=AG=4
过点A 作AB⊥对称轴于B
∴AB=2
在Rt△PAB中,BP=![]()
∴![]() (-2,3+
(-2,3+![]() )或
)或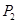 (-2,3-
(-2,3-![]() )……………………………6’
)……………………………6’
情况2:PG=AG=4
同理可得:![]() (-2,-1+
(-2,-1+![]() )或
)或![]() (-2,-1-
(-2,-1-![]() )…………………8’
)…………………8’
∴P点坐标为 (-2,3+![]() )或 (-2,3-
)或 (-2,3-![]() )或(-2,-1+
)或(-2,-1+![]() )或(-2,-1-
)或(-2,-1-![]() ).
).
解析:略


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:初中数学 来源: 题型:
 已知:如图,在梯形ABCD中,AD∥BC,AB=DC=8,对角线AC⊥AB,∠B=60°,M、N分别是边AB、DC的中点,连接MN,求线段MN的长.
已知:如图,在梯形ABCD中,AD∥BC,AB=DC=8,对角线AC⊥AB,∠B=60°,M、N分别是边AB、DC的中点,连接MN,求线段MN的长.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知,如图,在平面直角坐标系内,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(18,6).
已知,如图,在平面直角坐标系内,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(18,6).查看答案和解析>>
科目:初中数学 来源: 题型:
 (1)在△ABC中,AB=m2-n2,AC=2mn,BCm2+n2=(m>n>0).
(1)在△ABC中,AB=m2-n2,AC=2mn,BCm2+n2=(m>n>0).| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图,在公路OA、OB的交叉区域有P、Q两所学校,现要在其中建一个图书馆O′使它到两条公路的距离相等,到两所学校的距离也相等,在图中标出图书馆应建的位置O′.
已知:如图,在公路OA、OB的交叉区域有P、Q两所学校,现要在其中建一个图书馆O′使它到两条公路的距离相等,到两所学校的距离也相等,在图中标出图书馆应建的位置O′.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com