练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
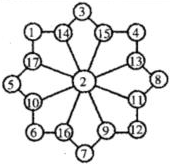
    8．如图，在17个小圆圈里分别填写着1至17这些自然数，每个小四边形上的4个数字之和都是34．想想看，如何调整一下这些数，使每个小四边形上的数字之和变为38？

    分析 首先根据图示，可得圆心处的数被加了8次，内圆上的8个数都被加了2次，外圆上的8个数都倍加了1次；然后求出1至17这17个自然数的和是多少，进而求出圆心处的数的7倍和内圆上的8个数的和是多少；最后确定中间的数字，调整各个位置上的数字，在17个小圆圈里分别填写着1至17这些自然数，每个小四边形上的4个数字之和都是38即可．

    解答 解：1+2+3+…+17
    =（1+17）×17÷2
    =18×17÷2
    =153，
    所以圆心处的数的7倍和内圆上的8个数的和是：
    38×8-153
    =304-153
    =151．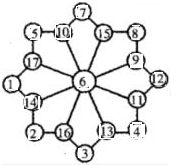

    点评 （1）此题主要考查了探寻数列规律问题，注意观察总结出规律，并能正确的应用规律，解答此题的关键是判断出：圆心处的数的7倍和内圆上的8个数的和是151．
    （2）此题是一道趣味数字游戏题，解题的关键是确定中间的数字，然后调整各个位置上的数字，需要有灵活的思维能力和钻研精神．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

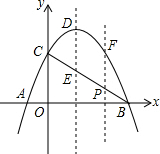    10．已知抛物线y=-x2+bx+c与x轴相交于A、B两点，与y轴相交于点C，且顶点为D（1，4）．
    （1）求b和c的值；
    （2）如图，连接BC，与抛物线的对称轴相交于点E，点P是线段BC上一动点，作点P作PF∥DF，交抛物线于点F，设点P的横坐标为m；
    ①用含m的代数式表示线段PF的长，并求当四边形DEPF为平行四边形时m的值；
    ②设△BCF的面积为S，求S与m的函数关系式，并求出s的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．已知x为实数，求代数式$\sqrt{x-4}$+$\sqrt{4-x}$-$\sqrt{2x}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

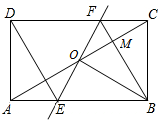    8．如图，矩形ABCD中，点O为AC的中点，过点O的直线分别与AB、CD交于点E、F，连接BF交AC于点M，连接DE、BO，若∠COB=60°，FO=FC．求证：
    （1）四边形EBFD是菱形；
    （2）BM：OE=3：2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．若x1，x2是方程2x2+x-3=0的两个根．
    （1）求x1+x2和x1x2的值．
    （2）求$\frac{1}{{{x}_{1}}}$+$\frac{1}{{{x}_{2}}}$的值．
    （3）求${{（{{x}_{1}}-{{x}_{2}}）}^{2}}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．解下列方程组
    （1）$\left\{{\begin{array}{l}{2x+3y=1}\\{5x-6y=7}\end{array}}\right.$
    （2）$\left\{{\begin{array}{l}{\frac{m}{2}+\frac{n}{3}=13}\\{\frac{m}{3}-\frac{n}{4}=3}\end{array}}\right.$
    （3）$\left\{{\begin{array}{l}{\frac{x+y}{2}=6-\frac{x-y}{3}}\\{4（x+y）-5（x-y）=2}\end{array}}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．方程组$\left\{\begin{array}{l}{3x-4y=2}\\{x+2y=1}\end{array}\right.$用代入法消去x，所得y的一元一次方程为（　　）
    A．3-2y-1-4y=2B．3（1-2y）-4y=2C．3（2y-1）-4y=2D．3-2y-4y=2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．（1）计算：（-1）2+sin230°+（$\sqrt{2}$）0-（$\frac{1}{2}$）-1
    （2）先化简，再求值：（$\frac{1}{a-2}$-$\frac{1}{a+2}$）÷$\frac{2}{2-a}$，其中a=$\sqrt{3}$-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．如图，DG∥BC，EF⊥AB，垂足分别为F，∠1=∠2，试证明CD是△ABC的高．

    查看答案和解析>>

    同步练习册答案