
分析 假设正确的时间为5时x分因为看到的时间比正确的时间早57分,所以看到的时间为4时(3+x)分,因为将时针及分针看错,所以5时x分的时针位置会和4时(3+x)分的分针位置重合,因为钟表一大格30°,时针一分钟走0.5度,分针一分钟走6° 也就是说,原时针到某时刻时的度数和新分针走的一样的度数,由此列出方程解答即可.
解答 解:假设正确的时间为5时x分,
因为看到的时间比正确的时间早57分,所以看到的时间为4时(3+x分,
因为将时针及分针看错,所以5时x分的时针位置会和4时(3+x)分的分针位置重合.
5×30+$\frac{1}{2}$x=6×(3+x)
解得x=24.
答:正确时间是5时24分.
点评 此题考查一元一次方程的实际运用,掌握钟表上时针、分针一分钟走的度数之间的关系是解决问题的关键.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
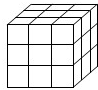 将一个正方体木块涂成红色,然后如图把它的棱三等分,再沿等分线把正方体切开,可以得到27个小正方体.观察并回答下列问题:
将一个正方体木块涂成红色,然后如图把它的棱三等分,再沿等分线把正方体切开,可以得到27个小正方体.观察并回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
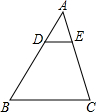 如图所示,若DE∥BC,$\frac{AD}{BD}=\frac{1}{2}$,求$\frac{{S}_{△ADE}}{{S}_{四边形BCED}}$.
如图所示,若DE∥BC,$\frac{AD}{BD}=\frac{1}{2}$,求$\frac{{S}_{△ADE}}{{S}_{四边形BCED}}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com