

分析 (1)以点O为圆心,以任意长为半径画弧与∠AOB的两边分别相交,再以两交点为圆心,以大于两交点之间的距离的一半为半径画弧,相交于一点,过这一点与O作射线OC即可;
(2)在OC上取一点P,使得OP=a;
(3)以O为圆心,以OD为半径作弧,交OA于E2,连接PE2,作PM⊥OA于M,PN⊥OB于N,根据角平分线上的点到角的两边的距离相等可得PM=PN,利用HL证明△E2PM≌△DPN,得出∠OE2P=∠ODP,再根据平角的定义即可求解.
解答 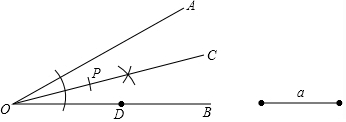 解:(1)如图,OC即为所求;
解:(1)如图,OC即为所求;
(2)如图,OP=a;
(3)∠OEP=∠ODP或∠OEP+∠ODP=180°.
理由是:以O为圆心,以OD为半径作弧,交OA于E2,连接PE2,作PM⊥OA于M,
PN⊥OB于N,则PM=PN.
在△E2PM和△DPN中,
$\left\{\begin{array}{l}{P{E}_{2}=PD}\\{PM=PN}\end{array}\right.$,
∴△E2PM≌△DPN(HL),
∴∠OE2P=∠ODP;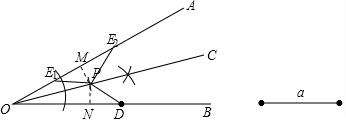 以P为圆心,以PD为半径作弧,交OA于另一点E1,连接PE1,
以P为圆心,以PD为半径作弧,交OA于另一点E1,连接PE1,
则此点E1也符合条件PD=PE1,
∵PE2=PE1=PD,
∴∠PE2E1=∠PE1E2,
∵∠OE1P+∠E2E1P=180°,
∵∠OE2P=∠ODP,
∴∠OE1P+∠ODP=180°,
∴∠OEP与∠ODP所有可能的数量关系是:∠OEP=∠ODP或∠OEP+∠ODP=180°.
点评 本题主要考查了角平分线的作法,作一个角等于已知角,过直线外一点作已知直线的垂线,都是基本作图,需要熟练掌握,另外还考查了角平分线上的点到角的两边的距离相等的性质,30°角所对的直角边等于斜边的一半的性质.


科目:初中数学 来源: 题型:选择题
| A. | 1.3008×106 | B. | 13.008×105 | C. | 1.3008×104 | D. | 0.13008×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6个 | B. | 5个 | C. | 4个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
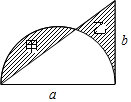 如图,已知直角三角形的两条直角边分别为a、b,以a为直径画一个半圆.若甲、乙两阴影部分的面积相等,则用a的代数式表示b=$\frac{1}{4}$πa.
如图,已知直角三角形的两条直角边分别为a、b,以a为直径画一个半圆.若甲、乙两阴影部分的面积相等,则用a的代数式表示b=$\frac{1}{4}$πa.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
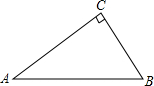 如图,某市把一块形状为直角三角形的废地开辟为生物园,∠ACB=90°,AC=80m,BC=60m.
如图,某市把一块形状为直角三角形的废地开辟为生物园,∠ACB=90°,AC=80m,BC=60m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com