
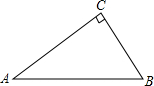
 如图,某市把一块形状为直角三角形的废地开辟为生物园,∠ACB=90°,AC=80m,BC=60m.
如图,某市把一块形状为直角三角形的废地开辟为生物园,∠ACB=90°,AC=80m,BC=60m.分析 (1)由题意可知:E点是AB的中点,则连接CE,CE是AB边的中线,则根据直角三角形中中线是斜边的一半;只要求得斜边AB的长即可,根据勾股定理可以求得AB的长;
(2)根据从一点到一直线垂线段线段的距离最短可知:从C点向AB作垂线,则CD的造价最低;根据三角形相似可以求得CD的长,AD的长;最后可以求得水渠的造价.
解答 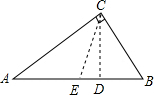 解:(1)过点C作CD⊥AB于D,取AB的中点为E,连接CE,
解:(1)过点C作CD⊥AB于D,取AB的中点为E,连接CE,
根据勾股定理可知:AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{8{0}^{2}+6{0}^{2}}$=100,
由题意可知:E点是AB的中点,
根据直角三角形中斜边上的中线是斜边的一半,
则CE=$\frac{1}{2}$AB=$\frac{1}{2}$×100=50m;
(2)由题意可知:从一点到一直线垂线段线段的距离最短,则从C点向AB作垂线,则CD的造价最低;
∵△ACB是直角三角形,CD⊥AB,
∴△ADC∽△ACB,
则$\frac{AC}{AB}$=$\frac{CD}{CB}$=$\frac{AD}{AC}$,
即$\frac{80}{100}$=$\frac{CD}{60}$=$\frac{AD}{80}$,
可解得:AD=64,CD=48;
则最低造价=10×48=480元.
答:点D在距点A64m处,此水渠的造价最低,最低造价是480元.
点评 本题考查的是勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 30cm | B. | 36cm | C. | 39cm | D. | 33cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
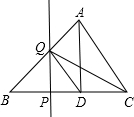 如图,△ABC中,AD⊥BC,垂足为D,AD=BD=3,CD=2,点P从点B出发沿线段BC的方向移动到点C停止,过点P作PQ⊥BC,交折线BA-AC于点Q,连接DQ、CQ,若△ADQ与△CDQ的面积相等,则线段BP的长度是( )
如图,△ABC中,AD⊥BC,垂足为D,AD=BD=3,CD=2,点P从点B出发沿线段BC的方向移动到点C停止,过点P作PQ⊥BC,交折线BA-AC于点Q,连接DQ、CQ,若△ADQ与△CDQ的面积相等,则线段BP的长度是( )| A. | $\frac{9}{5}$或4 | B. | $\frac{6}{5}$或4 | C. | $\frac{9}{5}$或$\frac{13}{5}$ | D. | $\frac{6}{5}$或$\frac{13}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,菱形纸片ABCD中,∠A=60°,将纸片折叠,点A,D分别落在A′,D′处,且A′D′经过点B,EF为折痕,当D′F⊥CD时,$\frac{CF}{BE}$的值为( )
如图,菱形纸片ABCD中,∠A=60°,将纸片折叠,点A,D分别落在A′,D′处,且A′D′经过点B,EF为折痕,当D′F⊥CD时,$\frac{CF}{BE}$的值为( )| A. | $\frac{3-\sqrt{3}}{2}$ | B. | $\frac{3+\sqrt{3}}{2}$ | C. | $\frac{3-\sqrt{3}}{3}$ | D. | $\frac{3+\sqrt{3}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
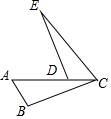 已知:如图,点A,D,C在同一直线上,AB∥EC,AC=CE,∠B=∠EDC.
已知:如图,点A,D,C在同一直线上,AB∥EC,AC=CE,∠B=∠EDC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com