
 如图,菱形纸片ABCD中,∠A=60°,将纸片折叠,点A,D分别落在A′,D′处,且A′D′经过点B,EF为折痕,当D′F⊥CD时,$\frac{CF}{BE}$的值为( )
如图,菱形纸片ABCD中,∠A=60°,将纸片折叠,点A,D分别落在A′,D′处,且A′D′经过点B,EF为折痕,当D′F⊥CD时,$\frac{CF}{BE}$的值为( )| A. | $\frac{3-\sqrt{3}}{2}$ | B. | $\frac{3+\sqrt{3}}{2}$ | C. | $\frac{3-\sqrt{3}}{3}$ | D. | $\frac{3+\sqrt{3}}{3}$ |
分析 作辅助线,构建直角三角形,设CF=x,FD=y,AE=a,则CD=x+y,根据菱形对角相等求得∠DCB=∠A=60°,由折叠得:∠BD′F=∠D=120°,则∠FD′M=60°,求得∠M=30°,根据30°的余切列式:tan30°=$\frac{D′F}{FM}$,得y=($\sqrt{3}$+1)x,再证明△A′EB也是60°的直角三角形,根据60°的余切列式并整理得出:AB=a+$\sqrt{3}$a,根据AB=CD列式:x+y=a+$\sqrt{3}$a,得出结论.
解答  解:延长FC、A′D′交于M,
解:延长FC、A′D′交于M,
设CF=x,FD=y,则CD=x+y,
∵四边形ABCD为菱形,∠A=60°,
∴AB∥CD,∠DCB=∠A=60°,
∴∠A+∠D=180°,
∴∠D=120°,
由折叠得:∠BD′F=∠D=120°,
∴∠FD′M=180°-120°=60°,
∵D′F⊥CD,
∴∠D′FC=90°,
∴∠M=90°-60°=30°,
在Rt△FOC中,∠DCB=60°,
∵∠DCB=∠CBM+∠M,
∴∠CBM=60°-30°=30°,
∴∠CBM=∠M,
∴CB=CM=x+y,
由折叠得:D′F=DF=y,
tan∠M=tan30°=$\frac{D′F}{FM}$,
∴$\frac{\sqrt{3}}{3}$=$\frac{y}{2x+y}$,
∴$\frac{x}{y}=\frac{\sqrt{3}-1}{2}$,
∴y=($\sqrt{3}$+1)x,
∵∠ABC=∠D=120°,∠CBM=30°,
∴∠ABM=120°+30°=150°,
∵∠A=∠A′=60°,
∴∠A′EB=150°-60°=90°,
设AE=a,则A′E=a,
tan∠A′=tan60°=$\frac{BE}{A′E}$=$\frac{BE}{a}$,
∴BE=$\sqrt{3}$a,
∵DC=AB,
∴x+y=a+$\sqrt{3}$a,
x+($\sqrt{3}$+1)x=($\sqrt{3}$+1)a,
$\frac{x}{a}$=$\frac{1+\sqrt{3}}{2+\sqrt{3}}$,
∴$\frac{x}{\sqrt{3}a}$=$\frac{1+\sqrt{3}}{2\sqrt{3}+3}$,
∴$\frac{FC}{BE}$=$\frac{x}{\sqrt{3}a}$=$\frac{1+\sqrt{3}}{2\sqrt{3}+3}$=$\frac{3-\sqrt{3}}{3}$.
故选C.
点评 本题考查了翻折变换和菱形的性质,及30°的直角三角形,从所要求比值的两条边入手,设未知数,作辅助线,构建直角三角形,根据菱形有关角的性质:菱形的对角相等、邻角互补,得出相应角的度数,利用特殊的三角函数值列式,并整理成方程求解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
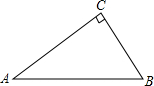 如图,某市把一块形状为直角三角形的废地开辟为生物园,∠ACB=90°,AC=80m,BC=60m.
如图,某市把一块形状为直角三角形的废地开辟为生物园,∠ACB=90°,AC=80m,BC=60m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
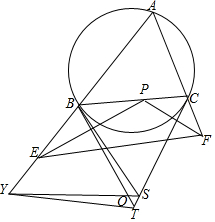 如图,在△ABC中,∠A=60°,P为线段BC(不含端点)上一点,E、F分别为射线AB、AC上的点,且BP=BE,CP=CF,△ABC的外接圆在B、C两点处的切线交于点S.设△EPF的外心为O,BO与CS交于点T,SO与直线AB交于点Y.求证:B、Y、T、S四点共圆.
如图,在△ABC中,∠A=60°,P为线段BC(不含端点)上一点,E、F分别为射线AB、AC上的点,且BP=BE,CP=CF,△ABC的外接圆在B、C两点处的切线交于点S.设△EPF的外心为O,BO与CS交于点T,SO与直线AB交于点Y.求证:B、Y、T、S四点共圆.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 观察下列每对数在数轴上的对应点之间的距离:4与-2,3与5,-2与-6,-4与3.并回答下列各题:
观察下列每对数在数轴上的对应点之间的距离:4与-2,3与5,-2与-6,-4与3.并回答下列各题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在边长为1个单位长度的小正方形组成的网格中,点A、B、C在小正方形的顶点上.
如图,在边长为1个单位长度的小正方形组成的网格中,点A、B、C在小正方形的顶点上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com