
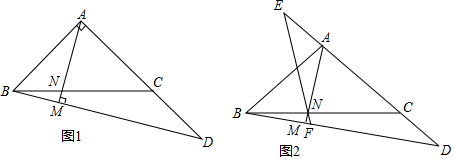
分析 (1)先判断出△ABC是等腰直角三角形,进而求出AB,BD,AD,最后根据等面积直接求出AM;
(2)先判断∠NBM=∠NAH=∠PCB,进而判断出△BHP≌△AHN,再判断出∠EAN=∠PCD,即可得出△AEN≌△CDP,最后用等角对等边即可;
(3)先判断出AC=2AE设出AE=a,进而表示出EQ,AD,再用等角的同名三角函数值相等,得出NR=$\frac{3}{2}$AR,即可表示出AR,RQ,最后代值即可.
解答 解:(1)在Rt△ABC中,AB=AC,
∴△ABC是等腰直角三角形,
∵BC=2$\sqrt{2}$,
∴AB=2,
∵∠ADB=30°,
∴BD=4,AD=2$\sqrt{3}$,
根据等面积法可得,AB•AD=AM•BD,
∴2×2$\sqrt{3}$=4•AM,
∴AM=$\sqrt{3}$,
(2)如图1,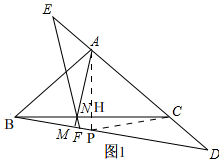
作AH⊥BC,AH延长线与BD交于P,连接CP,
∵△ABC是等腰直角三角形,
∴AH=BH=CH,BP=CP,∠PBC=∠PCB,
∵AM⊥BD,AH⊥BC,
∴∠BMN=∠AHN=90°,∠BNM=∠ANH,
∴∠NBM=∠NAH=∠PCB,
在△BHP和△AHN中,$\left\{\begin{array}{l}{∠NBM=∠NAH}\\{AH=BH}\\{∠BHP=∠AHN=90°}\end{array}\right.$,
∴△BHP≌△AHN,
∴BP=AN,
∴CP=AN,
∵∠PCB=∠PAM,
∴∠MAD=∠PAM+45°=∠PCB+45°=∠PCA,
∴∠EAN=∠PCD,
在△AEN和△CDP中,$\left\{\begin{array}{l}{CD=AE}\\{∠EAN=∠PCD}\\{AN=CP}\end{array}\right.$,
∴△AEN≌△CDP,
∴∠E=∠D,
∴EF=DF,
(3)如图2,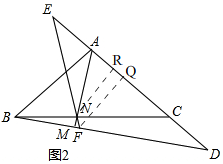
过点F作FQ⊥AC于Q,
由(2)可得,Q是DE的中点,
过N作NQ⊥AC于R,
设AE=a,
∵AE=$\frac{1}{2}$AC,
∴EQ=2a,AD=3a,
∴$\frac{NR}{AR}$=tan∠ABD=tan∠MAD=$\frac{AD}{EQ}$=$\frac{3}{2}$,
∵NR=CR,AC=AR+CR=2a,
∴$\frac{NR}{AR}=\frac{3}{2}$,
∴NR=$\frac{3}{2}$AR,
∴$\frac{3}{2}$AR+AR=2a,
∴AR=$\frac{4}{5}$a,
∴RQ=$\frac{1}{5}$a,
∴$\frac{EN}{NF}=\frac{ER}{RQ}=\frac{\frac{4}{5}a+a}{\frac{1}{5}a}$=$\frac{9}{1}$=9.
点评 此题是三角形综合题,主要考查了等腰直角三角形的判定和性质,全等三角形的判定和性质,锐角三角函数,解本题的关键是△BHP≌△AHN和∠EAN=∠PCD,作出辅助线是解本题的难点,是一道比较难的中考常考题.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:解答题
 试一试.
试一试.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 30cm | B. | 36cm | C. | 39cm | D. | 33cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,菱形纸片ABCD中,∠A=60°,将纸片折叠,点A,D分别落在A′,D′处,且A′D′经过点B,EF为折痕,当D′F⊥CD时,$\frac{CF}{BE}$的值为( )
如图,菱形纸片ABCD中,∠A=60°,将纸片折叠,点A,D分别落在A′,D′处,且A′D′经过点B,EF为折痕,当D′F⊥CD时,$\frac{CF}{BE}$的值为( )| A. | $\frac{3-\sqrt{3}}{2}$ | B. | $\frac{3+\sqrt{3}}{2}$ | C. | $\frac{3-\sqrt{3}}{3}$ | D. | $\frac{3+\sqrt{3}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
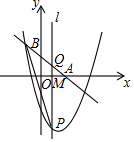 如图,已知直线y=-$\frac{3}{4}$x+1分别交x轴、y轴于点A、B,M是x轴正半轴上一动点,并以每秒1个单位的速度从O点向x轴正方向运动,过点M作x轴的垂线l,与抛物线y=x2-$\frac{5}{2}$x-2交于点P,与直线AB交于点Q,连结BP,经过t秒时,△PBQ是以BQ为腰的等腰三角形,则t的值是2或$\frac{3+\sqrt{21}}{2}$或$\frac{31}{8}$.
如图,已知直线y=-$\frac{3}{4}$x+1分别交x轴、y轴于点A、B,M是x轴正半轴上一动点,并以每秒1个单位的速度从O点向x轴正方向运动,过点M作x轴的垂线l,与抛物线y=x2-$\frac{5}{2}$x-2交于点P,与直线AB交于点Q,连结BP,经过t秒时,△PBQ是以BQ为腰的等腰三角形,则t的值是2或$\frac{3+\sqrt{21}}{2}$或$\frac{31}{8}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com