
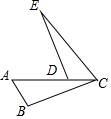
 已知:如图,点A,D,C在同一直线上,AB∥EC,AC=CE,∠B=∠EDC.
已知:如图,点A,D,C在同一直线上,AB∥EC,AC=CE,∠B=∠EDC.分析 (1)根据由两个角和其中一角的对边相等的两个三角形全等证明△ABC≌△CDE,由全等三角形的性质即可得到BC=DE;
(2)由三角形外家的性质可得∠ADE=∠BCE,根据全等三角形的性质即可证明
解答 证明:∵AB∥EC,
∴∠A=∠DCE,
在△ABC和△CDE中,
$\left\{\begin{array}{l}{∠B=∠EDC}\\{∠A=∠DCE}\\{AC=CE}\end{array}\right.$,
∴△ABC≌△CDE(AAS),
∴BC=DE;
(2)∠ADE=∠BCE,理由如下:
∵△ABC≌△CDE,
∴∠E=∠ACB,
∵∠ADE=∠E+∠ACE,∠BCE=∠ACB+∠ACE,
∴∠ADE=∠BCE.
点评 本题考查了全等三角形的判定和性质,全等三角形角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.


科目:初中数学 来源: 题型:解答题
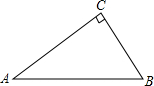 如图,某市把一块形状为直角三角形的废地开辟为生物园,∠ACB=90°,AC=80m,BC=60m.
如图,某市把一块形状为直角三角形的废地开辟为生物园,∠ACB=90°,AC=80m,BC=60m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 观察下列每对数在数轴上的对应点之间的距离:4与-2,3与5,-2与-6,-4与3.并回答下列各题:
观察下列每对数在数轴上的对应点之间的距离:4与-2,3与5,-2与-6,-4与3.并回答下列各题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 近似数3.20和近似数3.2都精确到十分位 | |
| B. | 近似数3.20×103和近似数3.2×103都精确到百位 | |
| C. | 近似数2千万和近似数2000万都精确到千万位 | |
| D. | 近似数32.0和近似数3.2都精确到十分位 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在边长为1个单位长度的小正方形组成的网格中,点A、B、C在小正方形的顶点上.
如图,在边长为1个单位长度的小正方形组成的网格中,点A、B、C在小正方形的顶点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com