
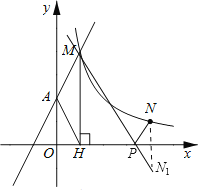
【题目】如图,直线y=2x+2与y轴交于A点,与反比例函数![]() (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(1)求k的值;
(2)点N(a,1)是反比例函数![]() (x>0)图象上的点在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.

【答案】(1)4;(2)存在,P点坐标为(![]() ,0).
,0).
【解析】试题分析:(1)根据直线解析式求A点坐标,得OA的长度;根据三角函数定义可求OH的长度,得点M的横坐标;根据点M在直线上可求点M的坐标.从而可求K的值;
(2)根据反比例函数解析式可求N点坐标;作点N关于x轴的对称点N1,连接MN1与x轴的交点就是满足条件的P点位置.
试题解析:(1)由y=2x+2可知A(0,2),即OA=2.
∵tan∠AHO=2,∴OH=1.
∵MH⊥x轴,∴点M的横坐标为1.
∵点M在直线y=2x+2上,
∴点M的纵坐标为4.即M(1,4).
∵点M在y=![]() 上,
上,
∴k=1×4=4.
(2)存在.
过点N作N关于x轴的对称点N1,连接MN1,交x轴于P(如图所示).此时PM+PN最小.
∵点N(a,1)在反比例函数y=![]() (x>0)上,
(x>0)上,
∴a=4.即点N的坐标为(4,1).
∵N与N1关于x轴的对称,N点坐标为(4,1),
∴N1的坐标为(4,-1).
设直线MN1的解析式为y=kx+b.
由![]()
解得k=-![]() ,b=
,b=![]() .
.
∴直线MN1的解析式为y=![]() x+
x+![]() .
.
令y=0,得x=![]() .
.
∴P点坐标为(![]() ,0).
,0).


科目:初中数学 来源: 题型:
【题目】如图,对面积为1的△ABC逐次进行以下操作:第一次操作,分别延长AB,BC,CA至点A1 , B1 , C1 , 使得A1B=2AB,B1C=2BC,C1A=2CA,顺次连接A1 , B1 , C1 , 得到△A1B1C1 , 记其面积为S1;第二次操作,分别延长A1B1 , B1C1 , C1A1至点A2 , B2 , C2 , 使得A2B1=2A1B1 , B2C1=2B1C1 , C2A1=2C1A1 , 顺次连接A2 , B2 , C2 , 得到△A2B2C2 , 记其面积为S2 , 则S2=。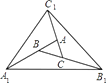
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把正整数1,2,3,4,…,2017排列成如下图所示的一个数表: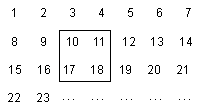
(1)用一正方形在表中随意框住4个数,把其中最小的数记为 ![]() ,另三个数用含
,另三个数用含 ![]() 的式子表示出来,从大到小依次是 , , ;
的式子表示出来,从大到小依次是 , , ;
(2)当被框住的4个数之和等于416时, ![]() 的值是多少?
的值是多少?
(3)被框住的4个数之和能否等于622?如果能,请求出此时 ![]() 的值;如果不能,请说明理由.
的值;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
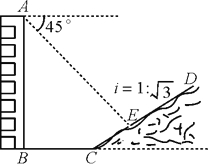
【题目】如图,一楼房AB后有一假山,其坡度为i=1∶![]() ,山坡坡面上E点处有一休息亭,测
,山坡坡面上E点处有一休息亭,测
得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角
为45°,求楼房AB的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,
在由边长都为1个单位长度的小正方形组成的 ![]() 正方形网格中,点A , B , P 都在格点上.请画出以AB为边的格点四边形(四个顶点都在格点的四边形),要求同时满足以下条件:
正方形网格中,点A , B , P 都在格点上.请画出以AB为边的格点四边形(四个顶点都在格点的四边形),要求同时满足以下条件:
条件1:点P到四边形的两个顶点的距离相等;
条件2:点P在四边形的内部或其边上;
条件3:四边形至少一组对边平行.
(1)在图①中画出符合条件的一个 ![]() ABCD , 使点P在所画四边形的内部;
ABCD , 使点P在所画四边形的内部;
(2)在图②中画出符合条件的一个四边形ABCD , 使点P在所画四边形的边上;
(3)在图③中画出符合条件的一个四边形ABCD , 使∠D=90°,且∠A≠90°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y1=-x2+4x和直线y2=2x.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1=y2,记M=y1=y2,下列判断:①当x>2时,M=y2;②当x<0时,x值越大,M值越大;③使得M大于4的x值不存在;④若M=2,则x=1.其中正确的有( )
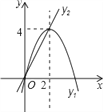
A. ③④ B. ②③ C. ②④ D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京等5个城市的国际标准时间(单位:小时)可在数轴上表示如下: ![]()
如果将两地国际标准时间的差简称为时差,那么下列说法中正确的是( )
A. 汉城与纽约的时差为13小时 B. 北京与纽约的时差为13小时
C. 北京与纽约的时差为14小时 D. 北京与多伦多的时差为14小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )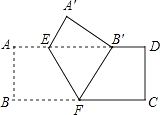
A.12
B.24
C.12 ![]()
D.16 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com