
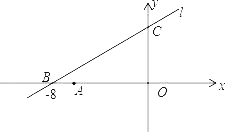
【题目】如图直线l:y=kx+6与x轴、y轴分别交于点B、C两点,点B的坐标是(﹣8,0),点A的坐标为(﹣6,0).
(1)求k的值.
(2)若点P是直线l在第二象限内一个动点,当点P运动到什么位置时,△PAC的面积为3,求出此时直线AP的解析式.
(3)在x轴上是否存在一点M,使得△BCM为等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
【答案】(1)![]() ,(2)P(﹣4,3);y=
,(2)P(﹣4,3);y=![]() x+9.(3)(﹣18,0),(﹣
x+9.(3)(﹣18,0),(﹣![]() ,0),(2,0)或(8,0),见解析.
,0),(2,0)或(8,0),见解析.
【解析】
(1)由点B的坐标,利用一次函数图象上点的坐标特征可求出k值;
(2)利用一次函数图象上点的坐标特征求出点C的坐标,设点P的坐标为(x,![]() x+6),由S△PAC=S△BOC﹣S△BAP﹣S△AOC结合△PAC的面积为3,可得出关于x的一元一次方程,解之即可得出点P的坐标,再利用待定系数法即可求出此时直线AP的解析式;
x+6),由S△PAC=S△BOC﹣S△BAP﹣S△AOC结合△PAC的面积为3,可得出关于x的一元一次方程,解之即可得出点P的坐标,再利用待定系数法即可求出此时直线AP的解析式;
(3)利用勾股定理求出BC的长度,分CB=CM,BC=BM,MB=MC三种情况考虑:①当CB=CM时,由OM1=OB=8可得出点M1的坐标;②当BC=BM时,由BM2=BM3=BC=10结合点B的坐标可得出点M2,M3的坐标;③当MB=MC时,设OM=t,则M4B=M4C=8﹣t,利用勾股定理可得出关于t的一元一次方程,解之即可得出点M4的坐标.综上,此题得解.
(1)∵直线l:y=kx+6过点B(﹣8,0),
∴0=﹣8k+6,
∴k=![]() .
.
(2)当x=0时,y=![]() x+6=6,
x+6=6,
∴点C的坐标为(0,6).
依照题意画出图形,如图1所示,
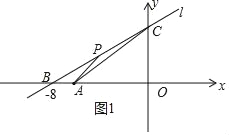
设点P的坐标为(x,![]() x+6),
x+6),
∴S△PAC=S△BOC﹣S△BAP﹣S△AOC,
=![]() ×8×6﹣
×8×6﹣![]() ×2(
×2(![]() x+6)﹣
x+6)﹣![]() ×6×6,
×6×6,
=﹣![]() x=3,
x=3,
∴x=﹣4,
∴点P的坐标为(﹣4,3).
设此时直线AP的解析式为y=ax+b(a≠0),
将A(﹣6,0),P(﹣4,3)代入y=ax+b,
得:![]() ,解得:
,解得: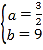 ,
,
∴当点P的坐标为(﹣4,3)时,△PAC的面积为3,此时直线AP的解析式为y=![]() x+9.
x+9.
(3)在Rt△BOC中,OB=8,OC=6,
∴BC=![]() =10.
=10.
分三种情况考虑(如图2所示):
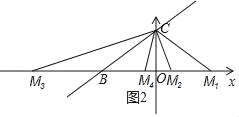
①当CB=CM时,OM1=OB=8,
∴点M1的坐标为(8,0);
②当BC=BM时,BM2=BM3=BC=10,
∵点B的坐标为(﹣8,0),
∴点M2的坐标为(2,0),点M3的坐标为(﹣18,0);
③当MB=MC时,设OM=t,则M4B=M4C=8﹣t,
∴CM42=OM42+OC2,即(8﹣t)2=t2+62,
解得:t=![]() ,
,
∴点M4的坐标为(﹣![]() ,0).
,0).
综上所述:在x轴上存在一点M,使得△BCM为等腰三角形,点M的坐标为(﹣18,0),(﹣![]() ,0),(2,0)或(8,0).
,0),(2,0)或(8,0).


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,AB=AC,点D、点O分别为BC、AC的中点,AE//BC.
(1)如图1,求证:四边形ADCE是矩形;
(2)如图2,若点 F是 CE上一动点,在不添加任何辅助线的情况下,请直接写出与四边形 ABDF 面积相等的三角形和四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在四边形ABCD中,AD∥BC,AB∥DC,点E在BC延长线上,连接DE,∠A+∠E=180°.
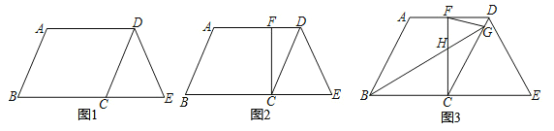
(1)如图1,求证:CD=DE;
(2)如图2,过点C作BE的垂线,交AD于点F,请直接写出BE、AF、DF 之间的数量关系_______________________;
(3)如图3,在(2)的条件下,∠ABC的平分线,交CD于G,交CF于H,连接FG,若∠FGH=45°,DF=8,CH=9,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂一周计划每日生产某产品100吨,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的吨数记为正数,减少的吨数记为负数)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减/吨 | ﹣1 | +3 | ﹣2 | +4 | +7 | ﹣5 | ﹣10 |
(1)生产量最多的一天比生产量最少的一天多生产多少吨?
(2)本周总生产量是多少吨?比原计划增加了还是减少了?增减数为多少吨?
(3)若本周总生产的产品全部由35辆货车一次性装载运输离开工厂,则平均每辆货车大约需装载多少吨?(结果精确到0.01吨)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】赵爽弦图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,若这四个全等直角三角形的两条直角边分别平行于x轴和y轴,大正方形的顶点B1、C1、C2、C3、…、Cn在直线y=﹣![]() 上,顶点D1、D2、D3、…、Dn在x轴上,则第n个阴影小正方形的面积为__.
上,顶点D1、D2、D3、…、Dn在x轴上,则第n个阴影小正方形的面积为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④BA+BC=2BF;其中正确的是( )
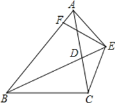
A.①②③B.①③④C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据图1,图2所提供的信息,解答下列问题:
(1)2007年海南省城镇居民人均可支配收入为 元,比2006年增长 %;
(2)求2008年海南省城镇居民人均可支配收入(精确到1元),并补全条形统计图;
(3)根据图1指出:2005﹣2008年海南省城镇居民人均可支配收入逐年 (填“增加”或“减少”).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知点A(-2,0).点D在y轴上,连接AD并将它沿x轴向右平移至BC的位置,且点B坐标为(4,0),连接CD,OD=![]() AB.
AB.
(1)线段CD的长为 ,点C的坐标为 ;
(2)如图2,若点M从点B出发,以1个单位长度/秒的速度沿着x轴向左运动,同时点N从原点O出发,以相同的速度沿折线OD→DC运动(当N到达点C时,两点均停止运动).假设运动时间为t秒.
①t为何值时,MN∥y轴;
②求t为何值时,S△BCM=2S△ADN.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com