A
分析:两组对边分别对应相等的四边形是平行四边形,平行四边形的两条对角线和它的四条边共构成4对全等的三角形.
解答:∵AB=CD,AD=BC
∴四边形ABCD是平行四边形,
∴OC=OA,OB=OD;
∵OD=OB,OB=OD,∠AOD=∠BOC;
∴△AOD≌△COB(SAS);①
同理可得出△AOB≌△COD(SAS);②
∵AD=BC,CD=AB,BD=BD;
∴△ABD≌△CDB(SSS);③
同理可得:△ABC≌△CDA(SSS).④
因此本题共有4对全等三角形.
故选择A.
点评:本题考查了对全等三角形的性质和判定,平行四边形的性质和判定等知识点的理解和运用,关键是根据平行四边形的性质得出边相等,再根据全等三角形的判定定理进行证明.全等三角形的判定方法有SSS,SAS,ASA,AAS.

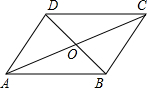 如图所示,AB=CD,AD=BC,则图中的全等三角形共有
如图所示,AB=CD,AD=BC,则图中的全等三角形共有
